题目内容
如图，△ABC内接于⊙O，AD平分∠BAC，交直线BC于点E，交⊙O于点D．
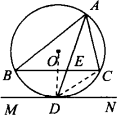
(1)过点D作MN∥BC，求证：MN是⊙O的切线；
(2)求证：AB·AC＝AD·AE；
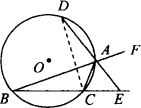
(3)如图，AE平分∠BAC的外角∠FAC，交BC的延长线于点E，EA的延长线交⊙O于点D．结论AB·AC＝AD·AE是否仍然成立？如果成立，请写出证明过程；如果不成立，请说明理由．
答案：
解析：
提示：
解析：
|
评析：用好圆中相等的圆周角，是圆中证明相似三角形的常用方法之一． |
提示：
|
第(1)题证明MN是⊙O的切线，需证MN⊥OD．第(2)(3)两题要证等积式，需寻求相似三角形来解决． |
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
15、如图，△ABC内接于⊙O，∠BAC=120°，AB=AC=4．BD为⊙O的直径，则BD=
21、如图，△ABC内接于⊙O，AB为⊙O的直径，点D在AB的延长线上，∠A=∠D=30°．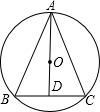
已知：如图，△ABC内接于⊙O，连接AO并延长交BC于点D，若AO=5，BC=8，∠ADB=90°，求△ABC的面积．
18、如图，△ABC内接于⊙O，∠A=30°，若BC=4cm，则⊙O的直径为（ ）
如图，△ABC内接于⊙O，AD⊥BC于点D，求证：∠BAD=∠CAO．