题目内容
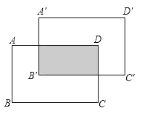
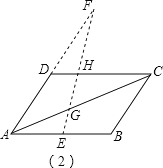
【题目】
ABCD中，点E是AB的中点，在直线AD上截取AF=2FD，EF交AC于G，则
=___________.
【答案】
或
【解析】①点F在线段AD上时，设EF与CD的延长线交于H，
∵AB∥CD，
∴△EAF∽△HDF，
∴HD：AE=DF：AF=1：2，
即HD=
AE，
∵AB∥CD，
∴△CHG∽△AEG，
∴AG：CG=AE：CH
∵AB=CD=2AE，
∴CH=CD+DH=2AE+
AE=
AE，
∴AG：CG=2：5，
∴AG：（AG+CG）=2：（2+5），
即AG：AC=2：7；
②点F在线段AD的延长线上时，设EF与CD交于H，
∵AB∥CD，
∴△EAF∽△HDF，
∴HD：AE=DF：AF=1：2，
即HD=
AE，
∵AB∥CD，
∴△CHG∽△AEG，
∴AG：CG=AE：CH
∵AB=CD=2AE，
∴CH=CD-DH=2AE-
AE=
AE，
∴AG：CG=2：3，
∴AG：（AG+CG）=2：（2+3），
即AG：AC=2：5，
故答案为： 
或
.
练习册系列答案
相关题目
