题目内容
请以-3和2.5为根,写出一个二次项系数不为1的一元二次方程________.
2x2+x- =0(答案不唯一)
=0(答案不唯一)
分析:因为方程有两根,所以△≥0;由于两根互为倒数,所以两根之积等于1,即二次项系数等于常数项.只要满足上述条件的方程即为所求.
解答:∵两根分别是-3和2.5,
∴- =-
=- ,
,
∴a=2b,即二次项系数等于一次项系数的2倍;
 =
=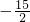 ,
,
∴c=- a,即常数项是二次项系数的-
a,即常数项是二次项系数的- ;
;
又∵方程有两不相等的实数根,
∴△>0;
因此可设方程为2ax2+ax- =0,且a2+60a>0,即a>0且a≠
=0,且a2+60a>0,即a>0且a≠ ,或a<-60;
,或a<-60;
如此方程可写为2x2+x- =0等.
=0等.
故答案是:2x2+x- =0(答案不唯一).
=0(答案不唯一).
点评:本题是一道开放题,考查的是一元二次方程的根与系数的关系.可用待定系数法求出方程.答案不唯一.
 =0(答案不唯一)
=0(答案不唯一)分析:因为方程有两根,所以△≥0;由于两根互为倒数,所以两根之积等于1,即二次项系数等于常数项.只要满足上述条件的方程即为所求.
解答:∵两根分别是-3和2.5,
∴-
 =-
=- ,
,∴a=2b,即二次项系数等于一次项系数的2倍;
 =
=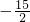 ,
,∴c=-
 a,即常数项是二次项系数的-
a,即常数项是二次项系数的- ;
;又∵方程有两不相等的实数根,
∴△>0;
因此可设方程为2ax2+ax-
 =0,且a2+60a>0,即a>0且a≠
=0,且a2+60a>0,即a>0且a≠ ,或a<-60;
,或a<-60;如此方程可写为2x2+x-
 =0等.
=0等.故答案是:2x2+x-
 =0(答案不唯一).
=0(答案不唯一).点评:本题是一道开放题,考查的是一元二次方程的根与系数的关系.可用待定系数法求出方程.答案不唯一.

练习册系列答案
相关题目