题目内容
5. 如图,直线l1过点A(0,2),点B(2,0),直线l2:y=$\frac{1}{2}$x+1与y轴交于点D,与x轴交于点E,两直线l1、l2相交于点C.
如图,直线l1过点A(0,2),点B(2,0),直线l2:y=$\frac{1}{2}$x+1与y轴交于点D,与x轴交于点E,两直线l1、l2相交于点C.(1)求直线l1的解析式和点C的坐标;
(2)求四边形OBCD的面积.
分析 (1)设直线l1的解析式为y=kx+b,由直线l2:y=kx+b经过点A(0,2),点B(2,0),得到方程组即可得到结论;
(2)求得D(0,1),解方程组得到C($\frac{2}{3}$,$\frac{4}{3}$),根据三角形的面积公式即可得到结论.
解答 解:(1)设直线l1的解析式为y=kx+b,
∵直线l2:y=kx+b经过点A(0,2),点B(2,0),
∴$\left\{\begin{array}{l}{2k+b=0}\\{b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
所以直线l1的解析式为y=-x+2;
(2)∵直线l2:y=$\frac{1}{2}$x+1与y轴交于点D,
∴D(0,1),
解$\left\{\begin{array}{l}{y=-x+2}\\{y=\frac{1}{2}x+1}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{4}{3}}\end{array}\right.$,
∴C($\frac{2}{3}$,$\frac{4}{3}$),
∴四边形OBCD的面积=S△AOB-S△ACD=$\frac{1}{2}×$2×2-$\frac{1}{2}$×$\frac{2}{3}$×$\frac{2}{3}$=$\frac{16}{9}$.
点评 本题考查了两直线相交的问题,主要利用了待定系数法求一次函数解析式,联立两函数解析式求交点坐标,三角形的面积,一定要熟练掌握并灵活运用.

练习册系列答案
相关题目
16.若a2bm+2与-2anb6是同类项,则m-n=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.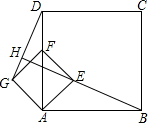 四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H,若AB=4,AE=$\sqrt{2}$时,则线段BH的长是( )
四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H,若AB=4,AE=$\sqrt{2}$时,则线段BH的长是( )
 四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H,若AB=4,AE=$\sqrt{2}$时,则线段BH的长是( )
四边形ABCD、AEFG都是正方形,当正方形AEFG绕点A逆时针旋转45°时,如图,连接DG、BE,并延长BE交DG于点H,且BH⊥DG与H,若AB=4,AE=$\sqrt{2}$时,则线段BH的长是( )| A. | $4\sqrt{2}$ | B. | 16 | C. | $\frac{{8\sqrt{10}}}{5}$ | D. | $\frac{{3\sqrt{10}}}{2}$ |
 如图,一个边长为a的正方形内画了一个圆,其直径也是a
如图,一个边长为a的正方形内画了一个圆,其直径也是a 如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N
如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N