题目内容
已知:如图,直线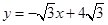 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.
相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.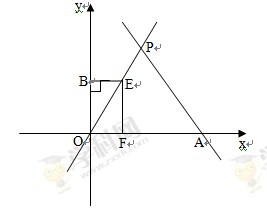
(1)求点P的坐标;
(2)请判断△OPA的形状并说明理由;
(3)请探究S与t之间的函数关系式,并指出t的取值范围.
(1)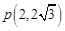 ;
;
(2)等边三角形;理由见解析;
(3) .
.
解析试题分析:(1)由两直线相交可列出方程组,求出P点坐标;
(2)将y=0代入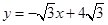 ,可求出OA=4,作PD⊥OA于D,则OD=2,PD=
,可求出OA=4,作PD⊥OA于D,则OD=2,PD=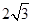 ,利用tan∠POA=
,利用tan∠POA=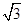 ,可知∠POA=60°,由OP=4.可知△POA是等边三角形;
,可知∠POA=60°,由OP=4.可知△POA是等边三角形;
(3)①当0<t≤4时,在Rt△EOF中,∠EOF=60°,OE=t,则EF=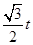 ,OF=
,OF= ,则S=
,则S=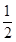 •OF•EF=
•OF•EF= ;
;
②当4<t<8时,设EB与OP相交于点C,易知:CE=PE=t﹣4,AE=8﹣t,可得AF=4﹣ ,EF=
,EF=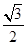 (8﹣t),有OF=OA﹣AF=4﹣(4﹣
(8﹣t),有OF=OA﹣AF=4﹣(4﹣ )=
)= ,S=
,S=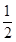 (CE+OF)•EF=﹣
(CE+OF)•EF=﹣ +4
+4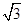 t﹣8
t﹣8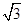 .
.
试题解析:(1)由题意可得: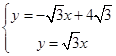 ,
,
解得 ,
,
所以点P的坐标为(2,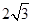 );
);
(2)将y=0代入y=﹣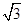 x+4
x+4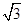 ,得到:﹣
,得到:﹣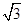 x+4
x+4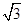 =0,
=0,
∴x=4,即OA=4,
作PD⊥OA于D,则OD=2,PD=2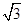 ,
,
∵tan∠POA= =
=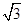 ,
,
∴∠POA=60°,
∵OP= ,
,
∴△POA是等边三角形;
(3)①当0<t≤4时,如图,在Rt△EOF中,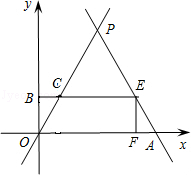
∵∠EOF=60°,OE=t,
∴EF=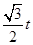 ,OF=
,OF= ,
,
∴S=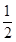 •OF•EF=
•OF•EF= .
.
②当4<t<8时,如图,设EB与OP相交于点C,
∵CE=PE=t﹣4,AE=8﹣t,
∴AF=4﹣ ,EF=
,EF=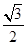 (8﹣t),
(8﹣t),
∴OF=OA﹣AF=4﹣(4﹣ )=
)= ,
,
∴S=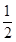 (CE+OF)•EF=
(CE+OF)•EF=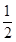 (t﹣4+
(t﹣4+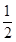 t)×
t)×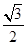 (8﹣t)=
(8﹣t)= 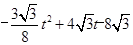 .
.
考点:一次函数综合题.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案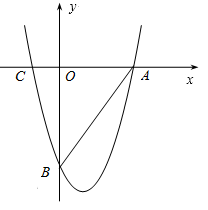
 .
. ;当x为何值时,
;当x为何值时, .
.

 为常数,且
为常数,且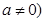 .
. 为何值,该函数的图象与
为何值,该函数的图象与 轴总有两个公共点;
轴总有两个公共点; 和点
和点 在抛物线
在抛物线 上.
上. 
 的值及点
的值及点 的坐标;
的坐标;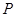 在
在 轴上,且满足△
轴上,且满足△ 是以
是以 为直角边的直角三角形,求点
为直角边的直角三角形,求点 ,点B的对应点为
,点B的对应点为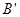 . 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,
. 点M(2,0)在x轴上,当抛物线向右平移到某个位置时, 最短,求此时抛物线的函数解析式.
最短,求此时抛物线的函数解析式. 的顶点在x轴上,且与y轴交于A点. 直线
的顶点在x轴上,且与y轴交于A点. 直线 经过A、B两点,点B的坐标为(3,4).
经过A、B两点,点B的坐标为(3,4).