题目内容
已知点 和点
和点 在抛物线
在抛物线 上.
上. 
(1)求 的值及点
的值及点 的坐标;
的坐标;
(2)点 在
在 轴上,且满足△
轴上,且满足△ 是以
是以 为直角边的直角三角形,求点
为直角边的直角三角形,求点 的坐标;
的坐标;
(3)平移抛物线 ,记平移后点A的对应点为
,记平移后点A的对应点为 ,点B的对应点为
,点B的对应点为 . 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,
. 点M(2,0)在x轴上,当抛物线向右平移到某个位置时, 最短,求此时抛物线的函数解析式.
最短,求此时抛物线的函数解析式.
(1)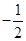 , B(-4,-8);(2)(0,0)或(0,-12);(3)右平移
, B(-4,-8);(2)(0,0)或(0,-12);(3)右平移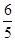 个单位时,抛物线的解析式为
个单位时,抛物线的解析式为 .
.
解析试题分析:(1)把点A(2,-2)代入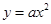 求出a=
求出a=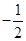 的值;把点B(-4,n)代入
的值;把点B(-4,n)代入 求得n=-8;
求得n=-8;
(2)先求出直线AB的解析式,然后进行分类讨论求出点P的坐标;
(3)利用对称性求解即可.
试题解析:(1)a=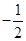
抛物线解析式为: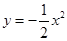
B(-4,-8);
(2) 记直线AB与x、y轴分别交于C、D两点,
则直线AB:y=x-4
C(4,0)、D(0,-4)
在Rt△COD中,∵OC=DO
∴∠ODA=45°
以A为直角顶点,则
在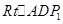 中,
中,
则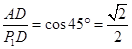
∴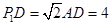
又∵D(0,-4)
∴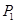 (0,0)
(0,0)
以B为直角顶点,则
在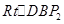 中,
中,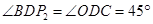
∴
∴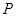 (0,-12)
(0,-12)
∴P(0,0)或(0,-12)
(3)记点A关于x轴的对称点为E(2,2)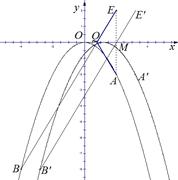
则BE:
令y=0,得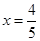
即BE与x轴的交点为Q(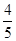 ,0)
,0)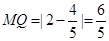
故抛物线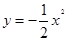 向右平移
向右平移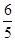 个单位时
个单位时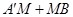 最短
最短
此时,抛物线的解析式为
考点:二次函数综合题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知抛物线 与
与 轴相交于
轴相交于 ,
, 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴相交于点
轴相交于点 .
.
(1)点 的坐标为 ,点
的坐标为 ,点 的坐标为 ;
的坐标为 ;
(2)在 轴的正半轴上是否存在点
轴的正半轴上是否存在点 ,使以点
,使以点 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出点
相似?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
(1)b= ,c= ;
(2)选取适当的数据填写下表,并在右图的直角坐标系中画出该函数的图像;
| x | … | | | | | | … |
| y | … | | | | | | … |
(3)若将此图象沿x轴向左平移3个单位,直接写出平移后图象所对应的函数关系式 .

 交
交 轴于A(2,0),B(6,0)两点,交
轴于A(2,0),B(6,0)两点,交 轴于点C(0,
轴于点C(0,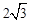 ).
).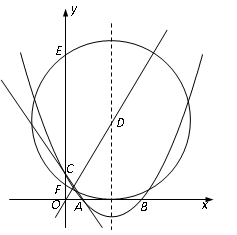
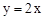 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交
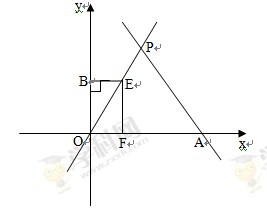
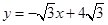 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.
相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.