题目内容
【题目】已知:梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别交射线
分别交射线![]() 、射线
、射线![]() 于点
于点![]() 、
、![]() .
.
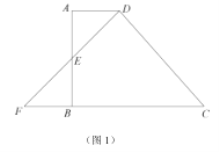
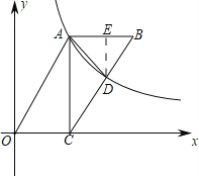
(1)当点![]() 为边
为边![]() 的中点时(如图1),求
的中点时(如图1),求![]() 的长:
的长:
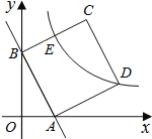
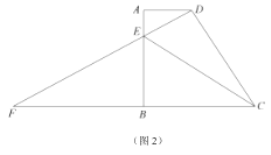
(2)当点![]() 在边
在边![]() 上时(如图2),联结
上时(如图2),联结![]() ,试问:
,试问:![]() 的大小是否确定?若确定,请求出
的大小是否确定?若确定,请求出![]() 的正切值;若不确定,则设
的正切值;若不确定,则设![]() ,
,![]() 的正切值为
的正切值为![]() ,请求出
,请求出![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)当![]() 的面积为3时,求
的面积为3时,求![]() 的面积.
的面积.
【答案】(1)9;(2)确定,![]() ;(3)25或73
;(3)25或73
【解析】
(1)证明△AED,△BEF,△DFC都是等腰直角三角形即可解决问题.
(2)如图2中,连接BD.取EC的中点O,连接OD,OB.证明E,B,C,D四点共圆,可得∠DCE=∠ABD即可解决问题.
(3)如图2﹣1中,连接AF.设AE=x,FB=y,EB=m,由S△AEF=![]() AEFB=3,推出xy=6,由AD∥FB,推出
AEFB=3,推出xy=6,由AD∥FB,推出![]() =
=![]() ,推出
,推出![]() =
=![]() ,可得xy=3m,推出6=3m,推出m=2,可得EB=2,AE=4,再利用勾股定理求出DE,DC即可解决问题.
,可得xy=3m,推出6=3m,推出m=2,可得EB=2,AE=4,再利用勾股定理求出DE,DC即可解决问题.
解:(1)如图1中,

∵AD∥BC,AB⊥BC,
∴∠ABC=∠A=90°,
∵AE=EB=3,AD=3,
∴AD=AE,
∴∠AED=∠ADE=∠BEF=∠F=45°,
∴EF=DE=3![]() ,FB=3,
,FB=3,
∵DF⊥DC,
∴∠FDC=90°,
∴∠C=∠F=45°,
∴DF=DC=6![]() ,
,
∴CF=![]() DC=12,
DC=12,
∴BC=CF﹣BF=12﹣3=9.
(2)结论::∠DCE的大小是定值.
理由:如图2中,连接BD.取EC的中点O,连接OD,OB.

∵∠EBC=∠EDC=90°,EO=OC,
∴OD=OE=OC=OB,
∴E,B,C,D四点共圆,
∴∠DCE=∠ABD,
∵在Rt△ADE中,tan∠ABD=![]() =
=![]() ,
,
∴∠ABDspan>的大小是定值,
∴∠DCE的大小是定值,
∴tan∠DCE=![]() .
.
(3)如图2﹣1中,连接AF.

设AE=x,FB=y,EB=m,
∵S△AEF=![]() AEFB=3,
AEFB=3,
∴xy=6,
∵AD∥FB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴xy=3m,
∴6=3m,
∴m=2,
∴EB=2,AE=4,
在Rt△AED中,DE=![]() =5,
=5,
在Rt△DEC中,∵tan∠DCE=![]() =
=![]() ,
,
∴DC=10,
∴S△DEC=![]() DEDC=
DEDC=![]() ×5×10=25.
×5×10=25.

 阅读快车系列答案
阅读快车系列答案