题目内容
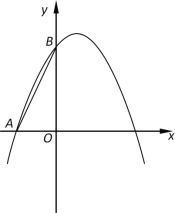
【题目】如图,抛物线![]() 经过点A(﹣2,0),点B(0,4).
经过点A(﹣2,0),点B(0,4).
(1)求这条抛物线的表达式;
(2)P是抛物线对称轴上的点,联结AB、PB,如果∠PBO=∠BAO,求点P的坐标;
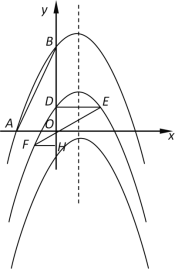
(3)将抛物线沿y轴向下平移m个单位,所得新抛物线与y轴交于点D,过点D作DE∥x轴交新抛物线于点E,射线EO交新抛物线于点F,如果EO=2OF,求m的值.
【答案】(1)![]() ;(2)P(1,
;(2)P(1,![]() ); (3)3或5.
); (3)3或5.
【解析】
(1)将点A、B代入抛物线![]() ,用待定系数法求出解析式.
,用待定系数法求出解析式.
(2)对称轴为直线x=1,过点P作PG⊥y轴,垂足为G, 由∠PBO=∠BAO,得tan∠PBO=tan∠BAO,即![]() ,可求出P的坐标.
,可求出P的坐标.
(3)新抛物线的表达式为![]() ,由题意可得DE=2,过点F作FH⊥y轴,垂足为H,∵DE∥FH,EO=2OF,∴
,由题意可得DE=2,过点F作FH⊥y轴,垂足为H,∵DE∥FH,EO=2OF,∴![]() ,∴FH=1.然后分情况讨论点D在y轴的正半轴上和在y轴的负半轴上,可求得m的值为3或5.
,∴FH=1.然后分情况讨论点D在y轴的正半轴上和在y轴的负半轴上,可求得m的值为3或5.
解:(1)∵抛物线经过点A(﹣2,0),点B(0,4)
∴![]() ,解得
,解得![]() ,
,
∴抛物线解析式为![]() ,
,
(2)![]() ,
,
∴对称轴为直线x=1,过点P作PG⊥y轴,垂足为G,
∵∠PBO=∠BAO,∴tan∠PBO=tan∠BAO,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∴P(1,![]() ),
),
(3)设新抛物线的表达式为![]()
则![]() ,
,![]() ,DE=2
,DE=2
过点F作FH⊥y轴,垂足为H,∵DE∥FH,EO=2OF
∴![]() ,
,
∴FH=1.
点D在y轴的正半轴上,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴m=3,
点D在y轴的负半轴上,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴m=5,
∴综上所述m的值为3或5.

练习册系列答案
相关题目