题目内容
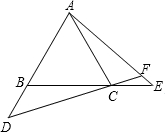
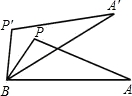
如图:已知在等边三角形ABC中,点D、E分别是AB、BC延长线上的点,且BD=CE,直线CD与AE相交于点F.
(1)求证:DC=AE;
(2)求证:AD2=DC•DF.
【考点】相似三角形的判定与性质;全等三角形的判定与性质;等边三角形的性质.
【分析】(1)利用“SAS”证明△DBC≌△ECA即可;
(2)由△DBC≌△ECA可知∠E=∠D,根据外角定理可知∠AFC=∠E+∠FCE=∠D+∠BCD=∠ABC=60°,可证△DCA∽△DAF,利用相似比得出结论.
【解答】证明:(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,BC=CA
∴∠DBC=∠ECA=180°﹣60°=120°
在△DBC与△ECA中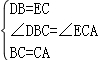
∴△DBC≌△ECA(SAS)
∴DC=AE;
(2)∵△DBC≌△ECA,
∴∠DCB=∠EAC
又∠ACB=∠BAC
∴∠DCA=∠DAF
又∠D=∠D
∴△DCA∽△DAF
∴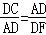
∴AD2=DC•DF.
【点评】本题考查了全等三角形、相似三角形的判定与性质.关键是根据等边三角形的性质找角相等的条件.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
 ,其中
,其中 .
.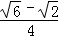 ,cos15°=
,cos15°=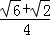 )
)
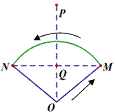
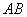 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段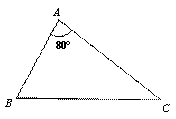
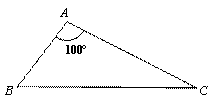
 (2)三角形的最小覆盖圆有何规律?请直接写出你所得到的结论(不要求证明);
(2)三角形的最小覆盖圆有何规律?请直接写出你所得到的结论(不要求证明); (其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
(其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.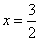 是关于
是关于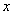 的方程
的方程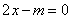 的解,则
的解,则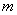 的值为 .
的值为 .