题目内容
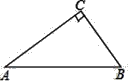
【题目】已知：如图，
，点
是
的中点，
平分
，
.
（1）求证：
；
（2）若
，试判断
的形状，并说明理由.
【答案】（1）见解析；（2）△ABC为等边三角形
【解析】
（1）根据三线合一定理，得AD⊥BD，由角平分线的性质定理，得BE=BD，即可得到
，即可得到结论；
（2）由BE∥AC，则∠EAC=∠E=90°，由角平分线的性质，得到∠EAB=∠BAD=∠CAD=30°，则∠BAC＝60°，即可得到答案.
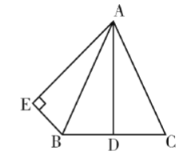
（1）证明：如图，
∵AB=AC ，点D是BC中点
∴AD⊥BD
∵AB平分∠DAE，AE⊥BE
∴BE=BD
∴
∴AD=AE；
（2）解：△ABC为等边三角形
∵BE∥AC
∴∠EAC=∠E=90°
∵AB=AC ，AD是中线
∴AD平分∠BAC
∵AB平分∠DAE
∴∠EAB=∠BAD=∠CAD=30°
∴∠BAC＝∠BAD+∠CAD＝60°
∵AB＝AC
∴△ABC是等边三角形.
练习册系列答案
名校课堂系列答案
相关题目
【题目】某超市计划购进甲、乙两种商品，两种商品的进价、售价如下表：
商品 | 甲 | 乙 |
进价（元/件） |
|
|
售价（元/件） | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同．
（1）求甲、乙两种商品的进价是多少元？
（2）若超市销售甲、乙两种商品共50件，其中销售甲种商品为
件（
），设销售完50件甲、乙两种商品的总利润为
元，求与之间的函数关系式，并求出的最小值．
