Question

【题目】已知不等臂跷跷板AB长为3米,跷跷板AB的支撑点O到地面上的点H的距高OH=0.6米。当跷跷板AB的一个端点A碰到地面时,AB与地面上的直线AH的夹角∠OAH的度数为30°.

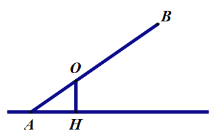
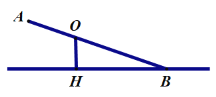
（1）当AB的另一个端点B碰到地面时(如右图）,跷跷板AB与直线BH的夹角∠ABH的正弦值是多少?

（2）当AB的另一个端点B碰到地面时(如右图),点A到直线BH的距离是多少米?

Answer 1

【答案】（1）；（2）1

【解析】

（1）先根据作图中求出OB的长度，再利用即可

（2）过A作AC⊥BH，垂足为点C.AC长即为所求.利用AB和即可求

解：(1)∵ ，OH=0.6

∴OA=1.2

∵AB=3m，AO=1.2m

∴OB=3-1.2=1.8m

在RtBOH中，

(2)过A作AC⊥BH，垂足为点C.AC长即为所求.

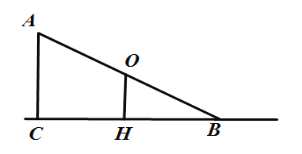
∴AC=AB=3×=1m.