Question

在平面直角坐标系中,点M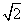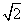（,）,以点M为圆心,OM长为半径作⊙M . 使⊙M与直线OM的另一交点为点B,与轴, 轴的另一交点分别为点D,A（如图）,连接AM.点P是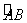上的动点.

（1）写出∠AMB的度数;

（2）点Q在射线OP上,且OP·OQ=20,过点Q作QC垂直于直线OM,垂足为C,直线QC交轴于点E.

①当动点P与点B重合时,求点E的坐标;

②连接QD,设点Q的纵坐标为,△QOD的面积为S.求S与的函数关系式及S的取值范围.

Answer 1

解：（1）90°；

（2）①由题意，易知：OM=2，OD=2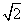，∴OB=4，

当动点P与点B重合时,∵OP·OQ=20，∴OQ=5，

∵∠OQE=90°，∠POE=45°，∴OE=5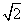，∴E点坐标为（5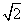，0）

②∵OD=2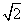，Q的纵坐标为,∴S=.

当动点P与B点重合时，过点Q作QF⊥轴，垂足为F点，∵OP=4，OP·OQ=20，∴OQ=5，

∵∠OFC=90°，∠QOD=45°，∴=，此时S=；

当动点P与A点重合时，Q点在轴上，∴OP=2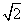，∵ OP·OQ=20，∴ =OQ=5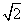，此时S=；

∴S的取值范围为.