题目内容
若x是一个不等于0的数,且x2-3x+1=0,则
等于( )
| x2 |
| x4+3x2+1 |
A、
| ||
B、
| ||
| C、10 | ||
| D、12 |
分析:由于x2-3x+1=0,那么有x+
=3,所求的式子分母复杂,考虑利用倒数法求解.先设,则
=z,则
=x2+3+
,再利用平方公式对式子x2+3+
变形,把x+
=3代入计算即可求
,再求倒数即可求z.
| 1 |
| x |
| x2 |
| x4+3x2+1 |
| 1 |
| z |
| 1 |
| x2 |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| z |
解答:解:设
=z,
则
=x2+3+
=(x+
)2+1,
∵x2-3x+1=0,
∴x+
=3,
∴
=32+1=10,
∴z=
.
故选A.
| x2 |
| x4+3x2+1 |
则
| 1 |
| z |
| 1 |
| x2 |
| 1 |
| x |
∵x2-3x+1=0,
∴x+
| 1 |
| x |
∴
| 1 |
| z |
∴z=
| 1 |
| 10 |
故选A.
点评:本题主要是利用倒数法求解,还用到了分式、完全平方公式的知识.

练习册系列答案
相关题目
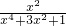 等于
等于
