题目内容
如图：已知：在△ABC中，AB=AC，BD⊥AC于D，若∠DBC=24°，则∠A=________．
48°
分析：首先利用直角三角形的性质求得∠C的度数，然后利用等腰三角形的性质求得结论即可．
解答：∵BD⊥AC于D，若∠DBC=24°，
∴∠C=90°-∠DBC=90°-24°=66°，
∵AB=AC，
∴∠ABC=∠C=66°，
∴∠A=180°-∠ABC-∠C=48°
故答案为48°．
点评：本题考查了直角三角形和等腰三角形的知识，属于基础题，相对比较简单．
分析：首先利用直角三角形的性质求得∠C的度数，然后利用等腰三角形的性质求得结论即可．
解答：∵BD⊥AC于D，若∠DBC=24°，
∴∠C=90°-∠DBC=90°-24°=66°，
∵AB=AC，
∴∠ABC=∠C=66°，
∴∠A=180°-∠ABC-∠C=48°
故答案为48°．
点评：本题考查了直角三角形和等腰三角形的知识，属于基础题，相对比较简单．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
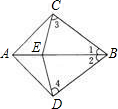
如图，已知：在Rt△ABC中，∠C=90°，E为AB的中点，且DE⊥AB于E，若∠CAD：∠DAB=1﹕2，求∠B的度数．
