题目内容
【题目】如图,![]() 内接于半圆,
内接于半圆,![]() 是直径,过
是直径,过![]() 作直线
作直线![]() ,
,![]() ,
,![]() 是弧
是弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(![]() )求证:
)求证:![]() 是半圆的切线.
是半圆的切线.
(![]() )作
)作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,试判断线段
,试判断线段![]() 与线段
与线段![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(![]() )若
)若![]() ,
,![]() ,试求
,试求![]() 的长.
的长.
【答案】(1)答案见解析;(2)AE=CH;(3)1.
【解析】试题分析:(1)由AB是直径得出∠ACB=90°,推出∠CAB+∠MAC=90°即可;
(2)连接AD,证明△ADE≌△CDH即可;
(3)由(2)可得出AE=CH,且DE=DH,可证得BE=BH,结合BC和AB的长可求出AE.
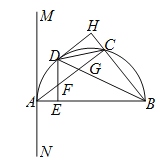
试题解析:解:(1)如图所示.∵AB是直径,∴∠ACB=90°,∴∠CAB+∠ABC=90°.∵∠MAC=∠ABC,∴∠CAB+∠MAC=90°,即∠MAB=90°,∴MN是半圆的切线;

(2)AE=CH.理由如下:
连接AD.∵D是弧AC的中点,∴AD=CD,∠HBD=∠ABD.∵DE⊥AB,DH⊥BC,∴DE=DH,∠AED=∠DHC,在Rt△ADE和Rt△CDH中,∵AD=CD,DE=DH,∴Rt△ADE≌Rt△CDH(HL),∴AE=CH;

(3)由(2)知DH=DE,∠DHB=∠DEB=90°,在Rt△DBH和Rt△DBE中,∵DH=DE,BD=BD,∴Rt△DBH≌Rt△DBE(HL),∴BE=BH,∴BA﹣AE=BC+CH,且AE=CH,∴BA﹣AE=BC+AE,又∵AB=6,BC=4,∴6﹣AE=4+AE,∴AE=1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目