题目内容
在△ABC中，D为AB的中点，AB=4，AC=7，若AC上有一点E，且△ADE与原三角形相似，则AE=．分析：在AC上有两点可构成三角形与原三角形相似：①若△ADE∽△ABC，可求AE=3.5；②若△ADE∽△ACB，可求AE=
．
| 8 |
| 7 |
解答：解：①若△ADE∽△ABC，
则AD：AB=AE：AC，
∵D为AB的中点，AB=4，AC=7，
∴AE=3.5；
②若△ADE∽△ACB，
则AD：AC=AE：AB，
∵D为AB的中点，AB=4，AC=7，
∴AE=
．
则AD：AB=AE：AC，
∵D为AB的中点，AB=4，AC=7，
∴AE=3.5；
②若△ADE∽△ACB，
则AD：AC=AE：AB，
∵D为AB的中点，AB=4，AC=7，
∴AE=
| 8 |
| 7 |
点评：在AC上有两点可构成三角形与原三角形相似．此题考查了学生的分析能力，考查了相似三角形的性质，相似三角形的对应角相等，对应边的比相等．
练习册系列答案
相关题目
已知：如图，在△ABC中，AD为BC边上的高，∠B=45°，∠C=30°，AD=2．求△ABC的面积．
AD于点F，交AE于点M，且∠B=∠CAE，FE：FD=4：3．
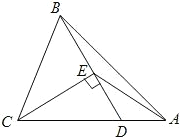
如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC面积是76cm2，AB=20cm，AC=18cm，求DE的长．