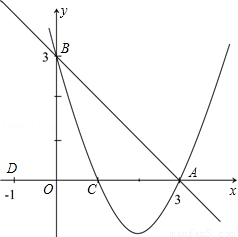
题目内容
已知:直线 交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线
交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线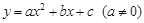 经过点A、B、C.
经过点A、B、C.
(1)求该抛物线的表达式;
(2)点D的坐标为(-3,0),点P为线段AB上一点,当锐角∠PDO的正切值为 时,求点P的坐标;
时,求点P的坐标;
(3)在(2)的条件下,该抛物线上的一点E在x轴下方,当△ADE的面积等于四边形APCE的面积时,求点E的坐标.
(1) ;(2)P(1,2);(3)
;(2)P(1,2);(3)
解析试题分析:(1)先求得直线 交x轴、y轴的交点A、B的坐标,即可求得点C的坐标,最后根据点A、B、C在抛物线
交x轴、y轴的交点A、B的坐标,即可求得点C的坐标,最后根据点A、B、C在抛物线 上,即可求得结果;
上,即可求得结果;
(2)由锐角∠PDO的正切值为 ,
, 得
得 ,即可证得△ABO∽△ADP,根据相似三角形的性质可得AP的长,过点P作
,即可证得△ABO∽△ADP,根据相似三角形的性质可得AP的长,过点P作 于点F,可证PF∥BO,即可证得
于点F,可证PF∥BO,即可证得 ,从而求得结果;
,从而求得结果;
(3)设点E的纵坐标为m(m<0),根据三角形的面积公式可得 ,即可得到
,即可得到 ,由
,由 即可列方程求解.
即可列方程求解.
(1)易得:A(2,0),B(0,4)
∵AC=1且OC<OA
∴点C在线段OA上
∴C(1,0)
∵A(2,0),B(0,4),C(1,0)在抛物线 上,
上,
∴ ,解得
,解得
∴所求抛物线的表达式为 ;
;
(2)∵锐角∠PDO的正切值为 ,
, (
( 为锐角)
为锐角)
∴ ,
,
∵点P为线段AB上一点,
∴
∴△ABO∽△ADP
∴ ,
,
又AO=2,AB= ,AD=5
,AD=5
∴
过点P作 于点F,可证PF∥BO,
于点F,可证PF∥BO,
∴
可得PF=2,即点P的纵坐标是2.
∴可得P(1,2);
(3)设点E的纵坐标为m(m<0),
∴
∵P(1,2),
∴
由 得
得 ,解得
,解得
∴点E  .
.
考点:二次函数的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 交x轴于
交x轴于 点A,交y轴于点
点A,交y轴于点 B,抛物线y=ax2+bx+c经过A(3,0),B(0,3),C(1,0)三点。
B,抛物线y=ax2+bx+c经过A(3,0),B(0,3),C(1,0)三点。 上有一点P,使△ABO与△ADP相似,求出点P的坐标;
上有一点P,使△ABO与△ADP相似,求出点P的坐标;  .
.


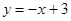 交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.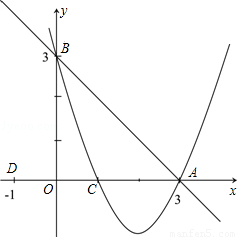
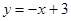 交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.