题目内容
利用配方法把二次函数y=-x2+4x+1化成y=a（x-h）2+k的形式．
分析：先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式．
解答：解：y=-x2+4x+1
=-（x2-4x+4）+1+4
=-（x-2）2+5．
所以把二次函数y=-x2+4x+1化成y=a（x-h）2+k的形式为：y=-（x-2）2+5．
=-（x2-4x+4）+1+4
=-（x-2）2+5．
所以把二次函数y=-x2+4x+1化成y=a（x-h）2+k的形式为：y=-（x-2）2+5．
点评：本题考查了二次函数的三种形式．二次函数的解析式有三种形式：
（1）一般式：y=ax2+bx+c（a≠0，a、b、c为常数）；
（2）顶点式：y=a（x-h）2+k；
（3）交点式（与x轴）：y=a（x-x1）（x-x2）．
（1）一般式：y=ax2+bx+c（a≠0，a、b、c为常数）；
（2）顶点式：y=a（x-h）2+k；
（3）交点式（与x轴）：y=a（x-x1）（x-x2）．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法，请你按有关内容补充完整：
| 复习日记卡片 |
| 内容：一元二次方程解法归纳 时间：2007年6月×日 |
| 举例：求一元二次方程x2-x-1=0的两个解 |
| 方法一：选择合适的一种方法（公式法、配方法、分解因式法）求解 解方程：x2-x-1=0． 解： |
方法二：利用二次函数图象与坐标轴的交点求解如图所示，把方程x2-x-1=0的解看成是二次函数y=  |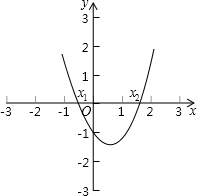
方法三：利用两个函数图象的交点求解 （1）把方程x2-x-1=0的解看成是一个二次函数y= （2）画出这两个函数的图象，用x1，x2在x轴上标出方程的解．  |
化成
的形式．