Question

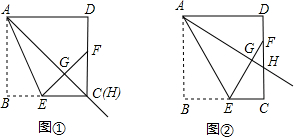
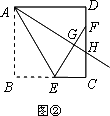
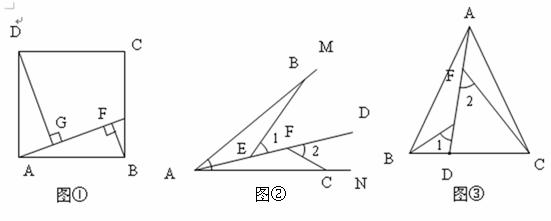
感知：如图①，点E在正方形ABCD的BC边上，BF⊥AE于点F，DG⊥AE于点G．可知△ADG≌△BAF.（不要求证明）

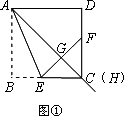
拓展：如图②，点B、C在∠MAN的边AM、AN上，点E, F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC,∠1=∠2=∠BAC.求证：△ABE≌△CAF.

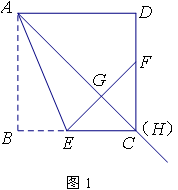
应用：如图③，在等腰三角形ABC中，AB=AC，AB＞BC．点D在边B上．CD=2BD.点E,  F在线段AD上．∠1=∠2=∠BAC．若△ABC的面积为9，则△ABE与△CDF的面积之和为_________.

Answer 1

解析：证明：如图②∵∠1=∠2=∠BAC  ∠1=∠BAE+∠EBA

                   ∠2=∠FCA+∠FAC  ∠BAC=∠BAE+∠FAC

                  ∴  ∠BAE=∠FCA    ∠ABE=∠FAC

                  ∵      AB=AC

                  ∴△ABE≌△CAF.

     解：如图③则△ABE与△CDF的面积之和为6.

     ∵由上题可知：△ABE≌△CAF.

     ∴△ABE与△CDF的面积之和=△CAF与△CDF的面积之和=△CAD的面积

     ∵  CD=2BD. △ABC的面积为9。

     ∴ △CAD的面积=6

     ∴△ABE与△CDF的面积之和为6.

考查知识：三角形全等的条件、三角形的面积计算、三角形的外角定理。