题目内容
如图:已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与A、C不重合),Q在BC上.
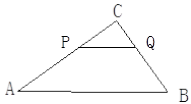
小题1:当△PQC的面积是四边形PABQ的面积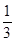 时,求CP的长
时,求CP的长
小题2:当△PQC的周长与四边形PABQ的周长相等时,求CP的长.
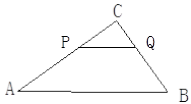
小题1:当△PQC的面积是四边形PABQ的面积
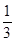 时,求CP的长
时,求CP的长小题2:当△PQC的周长与四边形PABQ的周长相等时,求CP的长.
小题1:∵PQ∥AB ∴△PQC∽△ABC
∵

∴

∴

∴
 …4分
…4分小题2:△PQC∽△ABC
∴

∴

∴

同理:

∴
 …………6分
…………6分 …………8′
…………8′∴

∴

∴
 …………10
…………10(1)由于PQ∥AB,故△PQC∽△ABC,当△PQC的面积是四边形以PABQ的面积 时,△CPQ与△CAB的面积比为1:4,根据相似三角形的面积比等于相似比的平方,可求出CP的长;
时,△CPQ与△CAB的面积比为1:4,根据相似三角形的面积比等于相似比的平方,可求出CP的长;
(2)由于△PQC∽△ABC,根据相似三角形的性质,可用CP表示出PQ和CQ的长,进而可表示出AP、BQ的长.根据△CPQ和四边形ABQP的周长相等,可将相关的各边相加,即可求出CP的长.
 时,△CPQ与△CAB的面积比为1:4,根据相似三角形的面积比等于相似比的平方,可求出CP的长;
时,△CPQ与△CAB的面积比为1:4,根据相似三角形的面积比等于相似比的平方,可求出CP的长;(2)由于△PQC∽△ABC,根据相似三角形的性质,可用CP表示出PQ和CQ的长,进而可表示出AP、BQ的长.根据△CPQ和四边形ABQP的周长相等,可将相关的各边相加,即可求出CP的长.

练习册系列答案
相关题目

 AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;



 中,线段
中,线段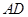 为其内角平分线,过
为其内角平分线,过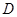 点的直线
点的直线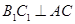 于
于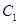 交
交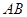 的延长线于
的延长线于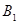 .
.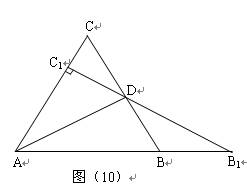
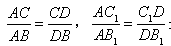 ,是否成立?
,是否成立?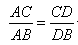 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.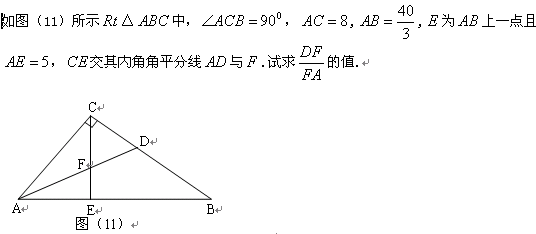
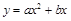 (a
(a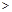 0)与双曲线
0)与双曲线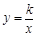 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).