题目内容
AB，CD是半径为5的⊙O中的两条平行弦，且AB=6，CD=8．则AB与CD之间的距离是________．
1或7
分析：过O作OE⊥CD于E，OE交AB于F，连接OD、OA、根据垂径定理求出AF、DE，根据勾股定理求出OE、OF，即可求出答案．
解答：
解：过O作OE⊥CD于E，OE交AB于F，连接OD、OA、
∵AB∥AC，
∴OE⊥AB，
∵OE⊥CD，OE过O，
∴DE=CE=
CD=4，
在Rt△ODE中，由勾股定理得：OE=
=3，
同理OF=4，
分为两种情况：
①如图1，EF=0E+OF=3+4=7；
②如图2，EF=OF-OE=4-3=1．
故答案为：1或7．
点评：本题考查了垂径定理和勾股定理的应用，用了分类讨论思想．
分析：过O作OE⊥CD于E，OE交AB于F，连接OD、OA、根据垂径定理求出AF、DE，根据勾股定理求出OE、OF，即可求出答案．
解答：
解：过O作OE⊥CD于E，OE交AB于F，连接OD、OA、∵AB∥AC，
∴OE⊥AB，
∵OE⊥CD，OE过O，
∴DE=CE=
CD=4，在Rt△ODE中，由勾股定理得：OE=
=3，同理OF=4，
分为两种情况：
①如图1，EF=0E+OF=3+4=7；
②如图2，EF=OF-OE=4-3=1．
故答案为：1或7．
点评：本题考查了垂径定理和勾股定理的应用，用了分类讨论思想．
练习册系列答案
相关题目
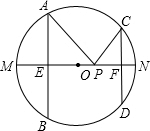如图，AB、CD是半径为5的⊙O的两条弦，AB=8，CD=6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上的任意一点，则PA+PC的最小值为
几何模型：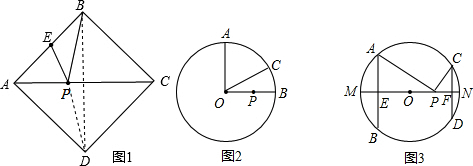
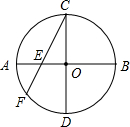如图所示，AB，CD是半径为5的圆内互相垂直的两条直径，E为AO的中点，连接CE并延长，交⊙O于另一点F，求弦CF的长．