题目内容
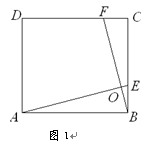
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.
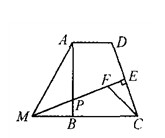
(1)若∠MFC=120°,求证:AM=2MB;
(2)求证:∠MPB=90°-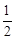 ∠FCM.
∠FCM.

(1)若∠MFC=120°,求证:AM=2MB;
(2)求证:∠MPB=90°-
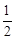 ∠FCM.
∠FCM. (1) 连结MD,
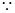 E是DC的中点,且ME⊥DC
E是DC的中点,且ME⊥DC
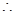 EM是CD的垂直平分线
EM是CD的垂直平分线
 MD=MC
MD=MC
△AMD和△FMC中
AM=FM
MD=MC
AD=FC
 △AMD
△AMD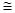 △FMC (SSS)
△FMC (SSS)

 MAD=
MAD= MFC=125
MFC=125
又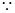 AD∥BC 且∠ABC=90
AD∥BC 且∠ABC=90

 BAD=90
BAD=90

 MAB=35
MAB=35
 MB=
MB=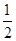 AM
AM
即MB=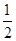 MF
MF
 MF=2MB
MF=2MB
(2) MD="MC" 且ME⊥DC
MD="MC" 且ME⊥DC
 ME平分
ME平分 DMC
DMC

 FMC=
FMC=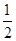
 DMC
DMC
又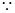 AD∥MC
AD∥MC

 DMC=
DMC= ADM
ADM
又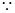 △AMD
△AMD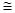 △FMC
△FMC

 ADM=
ADM= FCM
FCM

 DMC=
DMC= FCM
FCM

 FMC=
FMC=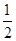
 FCM
FCM
Rt△BPM中
 MPB=90-
MPB=90- FMC
FMC
=90-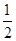
 FCM
FCM
 E是DC的中点,且ME⊥DC
E是DC的中点,且ME⊥DC EM是CD的垂直平分线
EM是CD的垂直平分线 MD=MC
MD=MC△AMD和△FMC中
AM=FM
MD=MC
AD=FC
 △AMD
△AMD △FMC (SSS)
△FMC (SSS)
 MAD=
MAD= MFC=125
MFC=125又
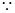 AD∥BC 且∠ABC=90
AD∥BC 且∠ABC=90
 BAD=90
BAD=90
 MAB=35
MAB=35 MB=
MB=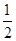 AM
AM即MB=
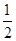 MF
MF MF=2MB
MF=2MB(2)
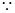 MD="MC" 且ME⊥DC
MD="MC" 且ME⊥DC  ME平分
ME平分 DMC
DMC
 FMC=
FMC=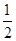
 DMC
DMC又
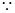 AD∥MC
AD∥MC
 DMC=
DMC= ADM
ADM又
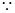 △AMD
△AMD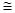 △FMC
△FMC
 ADM=
ADM= FCM
FCM
 DMC=
DMC= FCM
FCM
 FMC=
FMC=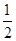
 FCM
FCMRt△BPM中
 MPB=90-
MPB=90- FMC
FMC=90-
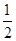
 FCM
FCM(1)连接MD,由于点E是DC的中点,ME⊥DC,所以MD=MC,然后利用已知条件证明△AMD≌△FMC,根据全等三角形的性质可以推出∴∠MAD=∠MFC=120°,接着得到∠MAB=30°,再根据30°的角所对的直角边等于斜边的一半即可证明AM=2BM;
(2)利用(1)的结论得到∠ADM=∠FCM,又AD∥BC,所以∠ADM=∠CMD,由此得到∠CMD=∠FCM,再利用等腰三角形的性质即可得到∠CME=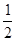 ∠FCM,再根据已知条件即可解决问题.
∠FCM,再根据已知条件即可解决问题.
(2)利用(1)的结论得到∠ADM=∠FCM,又AD∥BC,所以∠ADM=∠CMD,由此得到∠CMD=∠FCM,再利用等腰三角形的性质即可得到∠CME=
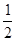 ∠FCM,再根据已知条件即可解决问题.
∠FCM,再根据已知条件即可解决问题.
练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 于
于 ,
, 的平分线
的平分线 交
交 于
于 ,交
,交 .求证:
.求证: .
.