题目内容
 如图所示,在小岛周围的
如图所示,在小岛周围的 | APB |
分析:此题主要是根据三角形的外角的性质:三角形的一个外角大于和它不相邻的内角,进行证明:一条弧所对的顶点在圆外的角都小于顶点在圆上的角;一条弧所对的顶点在圆内的角都大于顶点在圆上的角.
解答: 解:船在航行的过程中,始终保持对两灯塔A,B的视角小于θ,即可安全绕过暗礁区.
解:船在航行的过程中,始终保持对两灯塔A,B的视角小于θ,即可安全绕过暗礁区.
如右图所示,
(1)在
外任取一点C,连接CA,CB,
设CA交APB于F,连接FB.
∵∠AFB=θ,∠AFB>∠C
∴∠C<θ;
(2)在
内任取一点D,连接AD并延长交
于E,连接DB,EB
∵∠E=θ,∠ADB>∠E
∴∠ADB>θ
由(1)(2)知,在航标灯A,B所在直线的北侧,在圆弧
外任一点对A,B的视角都小于θ,在圆弧
上任一点对A,B的视角都等于θ,在圆弧
内任一点对A,B的视角都大于θ,为此,只有对两灯塔的视角小于θ的点才是安全点.
 解:船在航行的过程中,始终保持对两灯塔A,B的视角小于θ,即可安全绕过暗礁区.
解:船在航行的过程中,始终保持对两灯塔A,B的视角小于θ,即可安全绕过暗礁区.如右图所示,
(1)在
 |
| APB |
设CA交APB于F,连接FB.
∵∠AFB=θ,∠AFB>∠C
∴∠C<θ;
(2)在
 |
| APB |
 |
| APB |
∵∠E=θ,∠ADB>∠E
∴∠ADB>θ
由(1)(2)知,在航标灯A,B所在直线的北侧,在圆弧
 |
| APB |
 |
| APB |
 |
| APB |
点评:能够把数学和生活实际联系起来.注意:一条弧所对的圆外角总小于它所对的圆周角,它所对的圆内角总大于圆周角.

练习册系列答案
相关题目
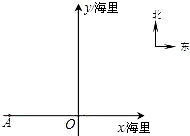 分钟后,渔船行至O处,此时看见小岛B在船的北偏东30°.在如图所示的坐标系中,点O为坐标原点,点A位于x轴上.
分钟后,渔船行至O处,此时看见小岛B在船的北偏东30°.在如图所示的坐标系中,点O为坐标原点,点A位于x轴上. 如图所示,海中有一座小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,B点测得小岛A在北偏东60°的方向上,航行12海里到达D点,这时测得小岛A在北偏东35°的方向上,如果渔船不改变航向,继续向东捕捞,有没有触礁的危险?
如图所示,海中有一座小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,B点测得小岛A在北偏东60°的方向上,航行12海里到达D点,这时测得小岛A在北偏东35°的方向上,如果渔船不改变航向,继续向东捕捞,有没有触礁的危险? 如图所示,在小岛周围的
如图所示,在小岛周围的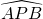 内有暗礁,在A,B两点建两座航标灯塔,且∠APB=θ,船要在两航标灯北侧绕过暗礁区,应怎样航行?为什么?
内有暗礁,在A,B两点建两座航标灯塔,且∠APB=θ,船要在两航标灯北侧绕过暗礁区,应怎样航行?为什么? 内有暗礁,在A,B两点建两座航标灯塔,且∠APB=θ,船要在两航标灯北侧绕过暗礁区,应怎样航行?为什么?
内有暗礁,在A,B两点建两座航标灯塔,且∠APB=θ,船要在两航标灯北侧绕过暗礁区,应怎样航行?为什么?