题目内容
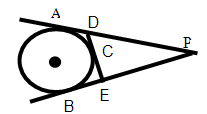
在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是_________
,则a的值是_________

 ,则a的值是_________
,则a的值是_________

解:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.

∵AB= ,
,
∴AE= ,PA=2,
,PA=2,
∴PE=1.
∵点A在直线y=x上,
∴∠AOC=45°,
∵∠DCO=90°,
∴∠ODC=45°,
∴∠PDE=∠ODC=45°,
∴∠DPE=∠PDE=45°,
∴DE=PE=1,
∴PD= .
.
∵⊙P的圆心是(2,a),
∴点D的横坐标为2,∵D在y=x的图象上,∴可得点D的纵坐标为2,
∴DC=2,
∴a=PD+DC=2+ .
.
故答案为2+ .
.

∵AB=
 ,
,∴AE=
 ,PA=2,
,PA=2,∴PE=1.
∵点A在直线y=x上,
∴∠AOC=45°,
∵∠DCO=90°,
∴∠ODC=45°,
∴∠PDE=∠ODC=45°,
∴∠DPE=∠PDE=45°,
∴DE=PE=1,
∴PD=
 .
.∵⊙P的圆心是(2,a),
∴点D的横坐标为2,∵D在y=x的图象上,∴可得点D的纵坐标为2,
∴DC=2,
∴a=PD+DC=2+
 .
.故答案为2+
 .
.
练习册系列答案
相关题目
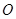 为△
为△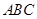 的外接圆,∠
的外接圆,∠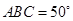 ,则∠
,则∠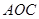 的度数为
的度数为
 中,
中, 以AC为直径作⊙O,交AB边于点D,过点O作OE∥AB,交BC边于点E.
以AC为直径作⊙O,交AB边于点D,过点O作OE∥AB,交BC边于点E. ,求AB的长.
,求AB的长. 





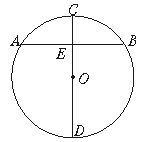
 是⊙
是⊙ 的直径,弦
的直径,弦 ,垂足为
,垂足为 ,如果
,如果 ,
, ,那么线段
,那么线段 的长是 .
的长是 .
 AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是______.
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是______.