题目内容
8. 如图,直线y=ax+b过点A(0,2)和点B(-3,0),若y>0时,x的取值范围是x>-3.
如图,直线y=ax+b过点A(0,2)和点B(-3,0),若y>0时,x的取值范围是x>-3.
分析 由点A、B的坐标利用待定系数法可求出直线AB的解析式,由a>0可得知y值随x值的增大而增大,结合点B的坐标即可得出当y>0时,x的取值范围.
解答 解:将点A(0,2)、B(-3,0)代入y=ax+b,
$\left\{\begin{array}{l}{b=2}\\{-3a+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=2}\end{array}\right.$,
∴直线AB的解析式为y=$\frac{2}{3}$x+2.
∵$\frac{2}{3}$>0,
∴y值随x值的增大而增大,
∴当x>-3时,y>0.
故答案为:x>-3.
点评 本题考查了待定系数法求一次函数解析式以及一次函数的性质,根据点A、B的坐标利用待定系数法求出直线AB的解析式是解题的关键.

练习册系列答案
相关题目
18.“神舟六号”宇航员费俊龙、聂海胜在太空共看到了76次日出日落,日行程约676000公里,用科学记数法表示日行程为( )
| A. | 6.76×107公里 | B. | 6.76×105公里 | C. | 0.676×106公里 | D. | 67.6×106公里 |
19.某电动自行车厂三月份的产量为1000辆,由于市场需求量不断增大,五月份的产量提高到l210辆,剩该厂四、五月份的月平均增长率为( )
| A. | 12.1% | B. | 20% | C. | 21% | D. | 10% |
16.下列事件为必然事件的有( )个
①过三点可以确定一个圆 ②平分弦的直径必垂直这条弦
③一个数的零次幂为零 ④两点确定一条直线.
①过三点可以确定一个圆 ②平分弦的直径必垂直这条弦
③一个数的零次幂为零 ④两点确定一条直线.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.下面四个图形中,可以看作是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
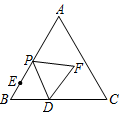 如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是8.
如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是8.