题目内容
14、一个三角形一边上的中线和另一边上的高所在直线分别是这个三角形的对称轴，则这个三角形是
等边
三角形．分析：根据对称轴的性质可得△ABD≌△ACD，△ABE≌△BCE，则AB=AC，AB=BC，即可证明△ABC为等边三角形．
解答：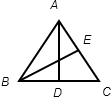
解：如图所示，AD是边BC上的高，BE是边AC边是的中线
∵AD，BE分别是三角形ABC的对称轴
∴△ABD≌△ACD，△ABE≌△BCE
∴AB=AC，AB=BC
∴AB=AC=BC
∴△ABC为等边三角形．
解：如图所示，AD是边BC上的高，BE是边AC边是的中线∵AD，BE分别是三角形ABC的对称轴
∴△ABD≌△ACD，△ABE≌△BCE
∴AB=AC，AB=BC
∴AB=AC=BC
∴△ABC为等边三角形．
点评：此题考查等边三角形的判定及对称轴的性质等知识点的掌握情况．
练习册系列答案
相关题目
下列说法中，正确的有（ ）
①有一个角为60°的等腰三角形是等边三角形
②三边分别是1，
，3的三角形是直角三角形
③一边上的中线等于这条边的一半的三角形是直角三角形
④三个角之比为3：4：5的三角形是直角三角形
①有一个角为60°的等腰三角形是等边三角形
②三边分别是1，
| 10 |
③一边上的中线等于这条边的一半的三角形是直角三角形
④三个角之比为3：4：5的三角形是直角三角形
| A、1个 | B、2个 | C、3个 | D、4个 |