题目内容
已知正三角形面积为
平方厘米,求正三角形的半径.
3
| ||
| 4 |
考点:正多边形和圆
专题:
分析:如图,求出BC=
OB,OD=
OB;根据正三角形面积为
平方厘米,列出关于线段OB的方程,问题即可解决.
| 3 |
| 1 |
| 2 |
3
| ||
| 4 |
解答: 解:如图,点O为正△ABC的中心,OD⊥BC;
解:如图,点O为正△ABC的中心,OD⊥BC;
则BD=CD;∠BOC=
×360°=120°,
∵OB=OC,
∴∠BOD=∠COD=
×120°=60°;
∴sin60°=
,
∴BD=
OB,BC=
OB;
同理可求:OD=
OB;
∵正三角形面积为
,
∴3×
×
OB•
OB=
,
解得:OB=
(厘米).
 解:如图,点O为正△ABC的中心,OD⊥BC;
解:如图,点O为正△ABC的中心,OD⊥BC;则BD=CD;∠BOC=
| 1 |
| 3 |
∵OB=OC,
∴∠BOD=∠COD=
| 1 |
| 2 |
∴sin60°=
| BD |
| OB |
∴BD=
| ||
| 2 |
| 3 |
同理可求:OD=
| 1 |
| 2 |
∵正三角形面积为
3
| ||
| 4 |
∴3×
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
3
| ||
| 4 |
解得:OB=
| ||||
| 3 |
点评:该题主要考查了正多边形和圆的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答;对分析问题解决问题的能力提出了一定的要求.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
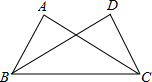 如图,∠A=∠D=90°,AC=DB,则△ABC≌△DCB的理由是( )
如图,∠A=∠D=90°,AC=DB,则△ABC≌△DCB的理由是( )| A、SAS | B、ASA |
| C、AAS | D、HL |
在平面直角坐标系中,点P(-2,-6)向左平移2单位,再向上平移3个单位后的点的坐标是( )
| A、(0,-3) |
| B、(-4,-3) |
| C、(0,-9) |
| D、(-4,-9) |
将二次根式
进行分母有理化的结果是( )
| ||
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,是由8个相同的小立方块搭成的几何体,它的三个视图是2×2的正方形.若拿掉若干个小立方块后(几何体不倒掉),其三个视图仍都为2×2的正方形,则最多能拿掉小立方块的个数为
如图,是由8个相同的小立方块搭成的几何体,它的三个视图是2×2的正方形.若拿掉若干个小立方块后(几何体不倒掉),其三个视图仍都为2×2的正方形,则最多能拿掉小立方块的个数为 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.