题目内容
 如图,∠ABE=∠C,AD∥BC,∠ADC的平分线交CB的延长线于点E,交AB于点F,试说明∠E=∠EFB.
如图,∠ABE=∠C,AD∥BC,∠ADC的平分线交CB的延长线于点E,交AB于点F,试说明∠E=∠EFB.考点:平行线的性质
专题:证明题
分析:先根据AD平行BC得出∠ADE=∠E.再由DE为∠ADC的平分可知∠1=∠2,故∠2=∠E.再根据∠ABE=∠C得出AB∥DC,故∠AFD=∠2,即∠E=∠AFD,根据∠EFB=∠AFD即可得出结论.
解答:证明:∵AD平行BC,
∴∠ADE=∠E.
又∵DE为∠ADC的平分线
∴∠1=∠2,
∴∠2=∠E.
∵∠ABE=∠C,
∴AB∥DC,
∴∠AFD=∠2,即∠E=∠AFD.
∵∠EFB=∠AFD,
∴∠E=∠EFB.
∴∠ADE=∠E.
又∵DE为∠ADC的平分线
∴∠1=∠2,
∴∠2=∠E.
∵∠ABE=∠C,
∴AB∥DC,
∴∠AFD=∠2,即∠E=∠AFD.
∵∠EFB=∠AFD,
∴∠E=∠EFB.
点评:本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
相关题目
-2-1=( )
| A、-1 | B、1 | C、3 | D、-3 |
 如图所示,在长为5cm,宽为3cm的长方形内部有一平行四边形,则平行四边形的面积为( )
如图所示,在长为5cm,宽为3cm的长方形内部有一平行四边形,则平行四边形的面积为( )| A、7cm2 |
| B、8cm2 |
| C、9cm2 |
| D、10cm2 |
 已知关于x的一元一次不等式2ax-a>-3的解集如图所示,则a的值为( )
已知关于x的一元一次不等式2ax-a>-3的解集如图所示,则a的值为( )| A、0 | B、1 | C、-1 | D、2 |
 如图,AB∥CD,AB∥EF,EG平分∠BED,∠B=45°,∠D=33°,求∠GEF的度数.
如图,AB∥CD,AB∥EF,EG平分∠BED,∠B=45°,∠D=33°,求∠GEF的度数.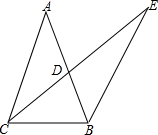 如图,已知AC=AB,AD=5,DB=4,∠A=2∠E.则CD•DE=
如图,已知AC=AB,AD=5,DB=4,∠A=2∠E.则CD•DE= 如图所示,将△ABC平移得到△A′B′C′,则图中与线段AA′平行且相等的线段为
如图所示,将△ABC平移得到△A′B′C′,则图中与线段AA′平行且相等的线段为