题目内容
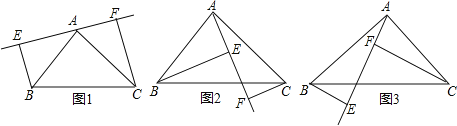
【题目】如图1,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.

(1)猜测∠1与∠2的关系,并说明理由;
(2)如果∠ABC是钝角,如图2,(1)中的结论是否还成立?
【答案】(1)∠1=∠2,理由见解析;(2)成立,理由见解析
【解析】
(1)根据垂直的定义可得△ABD和△BCE是直角三角形,再根据直角三角形两锐角互余可得∠1+∠B=90°,∠2+∠B=90°,从而得解;
(2)根据垂直的定义可得∠D=∠E=90°,然后求出∠1+∠CBE=90°,∠2+∠ABD=90°,再根据∠CBE、∠ABD是对顶角解答即可.
解:(1)∠1=∠2.理由如下:
∵AD⊥BC,CE⊥AB,
∴△ABD和△BCE都是直角三角形.
∴∠1+∠B=90°,∠2+∠B=90°.∴∠1=∠2.
(2)结论仍然成立.理由如下:
∵AD⊥BC,CE⊥AB,∴∠D=∠E=90°.
∴∠1+∠4=90°,∠2+∠3=90°.
∵∠3=∠4,
∴∠1=∠2.

 阅读快车系列答案
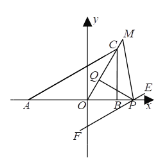
阅读快车系列答案【题目】祥云桥位于省城太原南部,该桥塔主体由三根曲线塔柱组合而成,全桥共设13对直线型斜拉索,造型新颖,是“三晋大地”的一种象征.某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
测量示意图 |
| 说明:两侧最长斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
38° | 28° | 234米 | |
… | … | ||
(1)请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)
(2)该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可).