Question

如下图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，∠DOE=90°

（1）求出∠AOD的补角的度数；

（2）试判断OE是否平分∠BOC，并说明理由。

 

Answer 1

【答案】

（1）∵OD平分∠AOC，

∴∠AOD=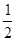∠AOC=25°，

∴∠BOD=180°-25°=155°

（2）OE平分∠BOC

理由：∵OD平分∠AOC，

∴∠COD=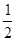∠AOC=25°，

又∵∠DOE=90°

∴∠COE=90°-25°=65°

又由（1）知∠BOD=155°

∴∠BOE=155°-90°=65°

∴∠BOE=∠COE

   ∴OE是平分∠BOC                                   

【解析】（1）由角平分线的性质即可推出∠AOD=25°，然后根据邻补角的性质即可推出∠BOD的度数，（2）首先根据垂线的性质和（1）所得的结论，即可推出∠COE和∠BOE的度数，然后根据角平分线的定义即可确定OE平分∠BOC．