Question

已知：如图，直线y=-

3

x+2

3

与x轴、y轴分别交于点A和点B，D是y轴上的一点，若将△DAB沿直线DA折叠，点B恰好落在x轴正半轴上的点C处，求直线CD的解析式．

Answer 1

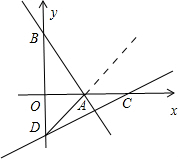
分析：由题意很容易看出A点坐标为（2，0），B点坐标为（0，2

3

），然后可以求出AB的长，C点坐标应该是OA+AB的长，Rt△DOC中，OD=OCtan∠DCO=2

3

，两点求解直线的解析式．

解答：解：根据题意，得：A（2，0），B（0，2

3

）
在Rt△AOB中，AB=

22+(2 3 )2

=4，∠DBA=30°
∴∠DCA=30°，OC=OA+AB=6
Rt△DOC中，OD=OCtan∠DCO=2

3

∴C（6，0），D（0，-2

3

）
设直线CD的解析式为：y=kx-2

3

∴0=6k-2

3

，解得k=

3

3

所以直线CD的解析式为y=

3

3

x-2

3

．

点评：解这类题要能够把题中的条件转化为图形上表达出来，折叠、重合等关键词的理解都是做题的关键所在，数形结合的思想对解题很有帮助．