题目内容
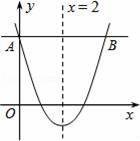
如图，已知抛物线y=x2+bx+c的对称轴为x=2，点A，B均在抛物线上，且AB与x轴平行，其中点A的坐标为（0，3），则点B的坐标为（ ）
A．（2，3） B．（3，2） C．（3，3） D．（4，3）
D【考点】二次函数的性质．
【专题】综合题．
【分析】已知抛物线的对称轴为x=2，知道A的坐标为（0，3），由函数的对称性知B点坐标．
【解答】解：由题意可知抛物线的y=x2+bx+c的对称轴为x=2，
∵点A的坐标为（0，3），且AB与x轴平行，
可知A、B两点为对称点，
∴B点坐标为（4，3）
故选D．
【点评】本题主要考查二次函数的对称性．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
x+3交AB，BC于点M，N，反比例函数y=
的图象经过点A（2，m），则m的值是（ ）
B．
C．3 D．2