Question

【题目】在平面直角坐标系中，中的点是边上的一点，过点的反比例函数与边交于点，连接.

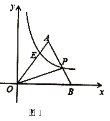
（1）如图1，若点的坐标为，点的坐标为，且的面积为5，求直线和反比例函数的解析式；

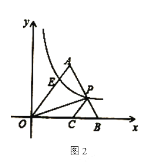
（2）如图2，若，过作，与交于点，若，并且的面积为，求反比例函数的解析式及点的坐标.

Answer 1

【答案】（1），；（2），，见解析.

【解析】

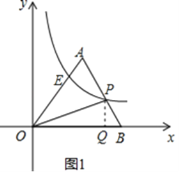
（1）过点P作PQ⊥x轴交x轴于点Q，利用待定系数法求出直线AB的解析式，根据△OPB的面积为5求出PQ的长，代入直线AB的解析式可得出P点坐标，进而可得出反比例函数的解析式；
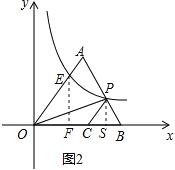
（2）过点E作EF⊥x轴交x轴于点F，过点P作PS⊥x轴交x轴于点S，利用锐角三角函数的定义求出OF及EF的长，故可得出反比例函数的解析式，根据△OPC的面积为 求出OCPS的长，再由锐角三角函数的定义得出PS的长，进而可得出P点坐标．

解：（1）如图1，过点作轴交轴于点，

点的坐标为，点的坐标为，

设直线的解析式为，

，解得，

直线的解析式为：.

点的坐标为，且的面积为5，

，点纵坐标为2.

点在直线上，解得.

点坐标为

此反比例函数的解析式为；

（2）如图2，过点作轴交轴于点，过点作轴交轴于点，

，

，

此反比例函数的解析式为.

，

.

，

，

，

，

，

.

点坐标为.