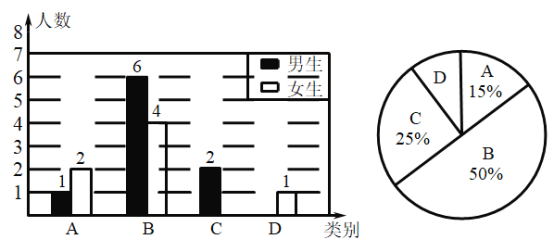
��Ŀ����
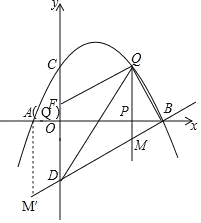
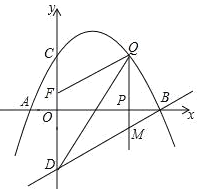
����Ŀ����ͼ����֪�����߾�����A����1��0����B��4��0����C��0��2�����㣬��D���C����![]() ��Գƣ���P��
��Գƣ���P��![]() ���ϵ�һ�����㣬���P������Ϊ��
���ϵ�һ�����㣬���P������Ϊ��![]() ��0��������P��
��0��������P��![]() ��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
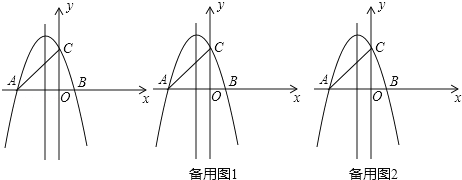
��1���������������ʾ�Ķ��κ����ı���ʽ��
��2����P���߶�AB�˶������У��Ƿ���ڵ�Q��ʹ����BOD�ס�QBM�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
��3����֪��F��0��![]() ��������P��
��������P��![]() �����˶�ʱ������
�����˶�ʱ������![]() Ϊ��ֵʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
Ϊ��ֵʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
���𰸡���1��![]() ����2�����ڣ�
����2�����ڣ�![]() ����3��-1��3��
����3��-1��3��![]() ��
��![]()
��������
��1�����ô���ϵ������⼴�ɣ�
��2����������ͼ��֪��DOB�ס�MBQ����MBQ�ס�QPB����BOD�ס�QPB������![]() ���ɵ������ɵ�
���ɵ������ɵ�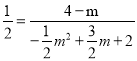 ����֮���ɵô�ʱmֵ��
����֮���ɵô�ʱmֵ��
��3�������ô���ϵ�������ֱ��BD�Ľ���ʽ�������õ���Q��M�����꣬����QM��DF���ı���DMQF��ƽ���ı���֪QM=DF���ݴ��г�����m�ķ��̣���֮����.
��1���������߹���A����1��0����B��4��0���������ʽΪy=a��x+1����x��4��������C��0��2�����룬�ã���4a=2����ã�a=��![]() ��
��
�������߽���ʽΪy=��![]() ��x+1����x��4��=��
��x+1����x��4��=��![]() ��
��
��2������ ��������
�ߡ�MBQ=90���MBP+��PBQ=90
�ߡ�MPB=��BPQ=90��
���MBQ+��BMP=90��
���PBQ=��BMP��
����MBQ�ס�QPB��
�ߡ�DOB�ס�MBQ��
���BOD�ס�QPB��
��![]() ����
����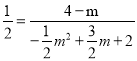 ��
��
��ã�m1=3��m2=4��
��m=4ʱ����P��Q��M�����B�غϣ����ܹ��������Σ���ȥ��
��m=3����Q��������3��2����
��3��������֪��D����Ϊ��0����2������ֱ��BD����ʽΪy=kx+b��
��B��4��0����D��0����2�����룬�ã�![]() ����ã�
����ã�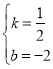 ��
��
��ֱ��BD����ʽΪy=![]() x��2����QM��x�ᣬP��m��0����
x��2����QM��x�ᣬP��m��0����
��Q��m��![]() ����M��m��
����M��m��![]() m��2����
m��2����
��QM=|![]() ����
����![]() m��2��|=|��
m��2��|=|��![]() m2+m+4|��
m2+m+4|��
��F��0��![]() ����D��0����2������DF=
����D��0����2������DF=![]() ����QM��DF��
����QM��DF��
�൱|��![]() m2+m+4|=
m2+m+4|=![]() ʱ���ı���DMQF��ƽ���ı��Σ���ã�m=��1��m=3��
ʱ���ı���DMQF��ƽ���ı��Σ���ã�m=��1��m=3��![]()
��m=��1��m=3��![]() ʱ���ı���DMQF��ƽ���ı��Σ�
ʱ���ı���DMQF��ƽ���ı��Σ�