Question

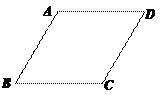
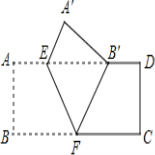
【题目】如图，将正方形ABCD折叠，使顶点A与CD边上的一点H重合（H不与端点C，D重合），折痕交AD于点E，交BC于点F，边AB折叠后与边BC交于点G，如果正方形ABCD的边长为1，则△CHG的周长为__________

Answer 1

【答案】2

【解析】分析：设CH=x，DE=y，则DH=1-x，EH=1-y，然后利用正方形的性质和折叠可以证明△DEH∽△CHG，利用相似三角形的对应边成比例可以把CG，HG分别用x，y分别表示，△CHG的周长也用x，y表示，然后在Rt△DEH中根据勾股定理可以得到2x-x2=2y，进而求出△CHG的周长．

详解：设CH=x，DE=y，则DH=1-x，EH=1-y，

∵∠EHG=90°，

∴∠DHE+∠CHG=90°．

∵∠DHE+∠DEH=90°，

∴∠DEH=∠CHG，

又∵∠D=∠C=90°，

∴△DEH∽△CHG，

∴CG：DH=CH：DE=HG：EH，即CG:(1x)=x:y=HG:(1y)，

∴CG=，HG=，

∴△CMG的周长为=CH+CG+HG=，

在Rt△DEH中，DH2+DE2=EH2,

即（1-x）2+y2=（1-y）2,

整理得2x-x2=2y，

∴CH+HG+CG=．

故答案为：2．