Question

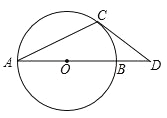
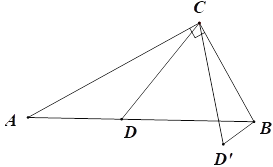
【题目】如图，在△ABC中，∠ACB=90°，∠A=30°，AB=6cm，点D是线段AB上一动点，将线段CD绕点C逆时针旋转50°至CD′，连接BD′．设AD为xcm，BD′为ycm．

小夏根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究.

下面是小夏的探究过程，请补充完整．

(1)通过取点、画图、测量，得到了与的几组值，如下表：

		1	2	3	3.5	4	5	6
	3.5		1.5	0.5	0.2	0.6	1.5	2.5

（说明：补全表格时相关数值保留一位小数）

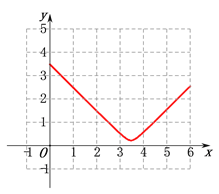
(2)建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；

(3)结合画出的函数图象，解决问题：当BD=BD'时，线段AD的长度约为_________.

Answer 1

【答案】（1）2.5；（2）见解析；（3）4.7

【解析】

（1）观察、分析表格中的数据可得：点（0，3.5），（2，1.5），（3，0.5）三个点在同一直线上，求出过这三点的直线的解析式，即可求得当x=1时的y的对应值；

（2）在所给方格纸中建立平面直角坐标系，然后根据表格中所给数据描出各点，并把各点用“平滑的曲线”连接起来即可；

（3）由题意可知，当BD=BD′时，6-x=y，即y=-x+6，在（2）中所得图象中画出直线y=-x+6的图象如下图1所示，则两个函数图象交点的横坐标为所求的x的值.

（1）设过点（2，1.5）和（3，0.5）的直线的解析式为y=kx+b，由此可得：

，解得： ，

∴过点（2，1.5）和（3，0.5）的直线的解析式为：y=-x+3.5，

∵当x=0时，y=3.5，

∴点（0，3.5）也在该直线上，

由此可知y与x的函数关系在的范围内是：y=-x+3.5，

∴当x=1时，y=-1+3.5=2.5，

∴将y=2.5填入表格的空格处即可；

（2）在方格纸中建立如下图所示的坐标系，然后按表格中所给数据描出各点，再将各点顺次连接，即可得到如下图所示的函数图象：

（3）∵BD=AB-AD=6-x，BD′=y，

∴当BD=BD′时，6-x=y，即：y=-x+6，

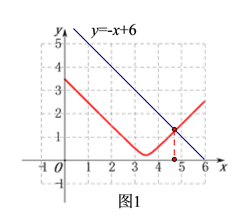
在（2）所得的函数坐标系中画出直线y=-x+6的图象（如图1所示），则两个函数图象的交点的横坐标即为BD=BD′时的x的值，

由下图可得：两函数图象交点的横坐标约为：4.7，

∴当BD=BD′时，x=4.7，即此时BD的长约为4.7cm.