题目内容
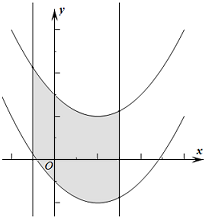 如图,两条抛物线y1=
如图,两条抛物线y1=| 1 |
| 2 |
| 1 |
| 2 |
| A、6 | B、8 | C、10 | D、4 |
考点:二次函数图象与几何变换
专题:
分析:两函数差的绝对值乘以两条直线的距离即可得到所求的阴影部分的面积.
解答:解:∵两解析式的二次项系数相同,
∴两抛物线的形状完全相同,
∴y1-y2=
(x-1)2+1-
(x-1)2+1=2,
∴S阴影=(y1-y2)×|3-(-1)|=2×4=8.
故选:B.
∴两抛物线的形状完全相同,
∴y1-y2=
| 1 |
| 2 |
| 1 |
| 2 |
∴S阴影=(y1-y2)×|3-(-1)|=2×4=8.
故选:B.
点评:此题主要考查了二次函数图象与几何变换.此题是利用二次函数图象的特点与分割拼凑的方法求不规则图形的面积.

练习册系列答案
相关题目
若ab<0,则函数y=-
(a、b为常数)的图象( )
| b |
| ax |
| A、在第一、三象限 |
| B、在第二、四象限 |
| C、平行于x轴 |
| D、平行于y轴 |
若
=-a
,那么实数a的取值范围是( )
| a3+a2 |
| a+1 |
| A、a<-1 | B、a>0 |
| C、0<a≤1 | D、-1≤a≤0 |
 如图,M、N、P、R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1.数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=3,则原点是( )
如图,M、N、P、R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1.数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=3,则原点是( ) 如图,直线l1与l2相交于点P,直线l1的表达式为y=2x+3,P点的横坐标为-1,且l2交y轴于点A(0,1),求直线l2的函数表达式.
如图,直线l1与l2相交于点P,直线l1的表达式为y=2x+3,P点的横坐标为-1,且l2交y轴于点A(0,1),求直线l2的函数表达式.