题目内容
已知：如图，⊙A的圆心为（4，0），半径为2，OP切⊙A于P点，则阴影部分的面积为
- A.
- B.
- C.
- D.
A
分析：易得△OAP为直角三角形，利用勾股定理可求得另一直角边，利用相应的三角函数可求得∠OAP的度数．
S阴影=S△OAP-S扇形．
解答：连接AP，则∠OPA=90°．
∵AP=2，OA=4，
∴OP=2
，∠OAP=60°，
∴S阴影=S△OAP-S扇形=
×AP•OP-
=．
故选A．
点评：本题利用了直角三角形的性质，勾股定理，扇形的面积公式求解．
分析：易得△OAP为直角三角形，利用勾股定理可求得另一直角边，利用相应的三角函数可求得∠OAP的度数．
S阴影=S△OAP-S扇形．
解答：连接AP，则∠OPA=90°．
∵AP=2，OA=4，
∴OP=2
，∠OAP=60°，∴S阴影=S△OAP-S扇形=
×AP•OP-=．故选A．
点评：本题利用了直角三角形的性质，勾股定理，扇形的面积公式求解．
练习册系列答案
相关题目
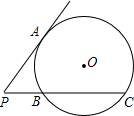已知：如图，PA是圆的切线，A为切点，PBC是圆的割线，且BC=2PB，求
此抛物线上，矩形面积为12，
已知：如图，圆锥的母线长OA=6，底面圆的半径为