题目内容
 如图,在⊙O中,
如图,在⊙O中, ,给出下列三个结论:
,给出下列三个结论:
(1)DC=AB;(2)AO⊥BD;(3)当∠BDC=30°时,∠DAB=80°.
其中正确的个数是
- A.0
- B.1
- C.2
- D.3
D
分析:先根据 ,得出DC=AB和AO⊥BD,再设出设∠DBC=x度,则由△DBC的内角和为180°得出x的值,即可求出答案;
,得出DC=AB和AO⊥BD,再设出设∠DBC=x度,则由△DBC的内角和为180°得出x的值,即可求出答案;
解答:连接OB,OD,延长AO与BD交于点E,如图所示:
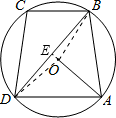
∵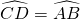 ,
,
∴DC=AB;
∵ ,
,
∴AB=AD,
∵AO是半径,OB=OD,
∴△ABO≌△ADO(SSS),
∴∠DAO=∠BAO,又AB=AD,
∴AE⊥BD,即AO⊥BD;
∵ =2
=2 ,
,
∴∠C=2∠DBC,
设∠DBC=x,则∠C=2∠DBC=2x,
由△DBC的内角和为180°得:
3x+30°=180°,
解得:x=50°,
∴∠C=100°,
∴∠DAB=80°;
故选D.
点评:此题考查了圆心角、弧、弦的关系;解题的关键是根据已知条件和三角形内角和等于180度进行解答,比较容易.
分析:先根据
 ,得出DC=AB和AO⊥BD,再设出设∠DBC=x度,则由△DBC的内角和为180°得出x的值,即可求出答案;
,得出DC=AB和AO⊥BD,再设出设∠DBC=x度,则由△DBC的内角和为180°得出x的值,即可求出答案;解答:连接OB,OD,延长AO与BD交于点E,如图所示:

∵
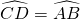 ,
,∴DC=AB;

∵
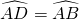 ,
,∴AB=AD,
∵AO是半径,OB=OD,
∴△ABO≌△ADO(SSS),
∴∠DAO=∠BAO,又AB=AD,
∴AE⊥BD,即AO⊥BD;
∵
 =2
=2 ,
,∴∠C=2∠DBC,
设∠DBC=x,则∠C=2∠DBC=2x,
由△DBC的内角和为180°得:
3x+30°=180°,
解得:x=50°,
∴∠C=100°,
∴∠DAB=80°;
故选D.
点评:此题考查了圆心角、弧、弦的关系;解题的关键是根据已知条件和三角形内角和等于180度进行解答,比较容易.

练习册系列答案
相关题目
 ∠ACB的外角平分线于点F.
∠ACB的外角平分线于点F. 14、如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,下面给出三个结论:
14、如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,下面给出三个结论: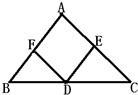 18、如图,在△ABC中,D为BC边的中点,过D点分别作DE∥AB交AC于点E,DF∥AC交AB于点F.
18、如图,在△ABC中,D为BC边的中点,过D点分别作DE∥AB交AC于点E,DF∥AC交AB于点F. 已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D.
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D.