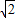题目内容
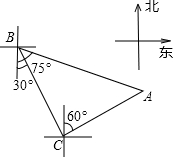 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )
轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )A、25
| ||
B、25
| ||
| C、50海里 | ||
| D、25海里 |
分析:根据方向角的定义得出∠ACB的度数以及BC的长,进而得出AC的长.
解答:解:∵轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,
在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,
∴BC=25海里,∠ABC=75°-30°=45°,
∵在C处观测灯塔A位于北偏东60°方向上,
∴∠BCA=90°,
∴△ACB是等腰直角三角形,
∴BC=AC=25(海里).
故选:D.
在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,
∴BC=25海里,∠ABC=75°-30°=45°,
∵在C处观测灯塔A位于北偏东60°方向上,
∴∠BCA=90°,
∴△ACB是等腰直角三角形,
∴BC=AC=25(海里).
故选:D.
点评:此题主要考查了方向角的确定以及等腰直角三角形的性质,根据题意得出△ABC的形状是解题关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目

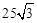 B.
B. C.50
D.25
C.50
D.25