题目内容
如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE
(1)求证:△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
(1)见解析(2)  解析:
解析:
证明:(1)∵点 是线段
是线段 的中点,
的中点,
∴
又∵ 平分
平分
 平分
平分
∴
∴ (2分)
(2分)
在 和
和 中,
中,

∴ (4分)
(4分)
(2)解:∵
∴
∵ (7分)
(7分)
∴
∴ (8分)
(8分)
(1)先利用角平分线性质、以及等量代换,可证出∠1=∠3,结合CD=CE,C是AB中点,即AC=BC,利用SAS可证全等;(2)利用角平分线性质,可知∠1=∠2,∠2=∠3,从而求出∠1=∠2=∠3,再利用全等三角形的性质可得出∠E=∠D,在△BCE中,利用三角形内角和是180°,可求出∠B
 解析:
解析:证明:(1)∵点
 是线段
是线段 的中点,
的中点,∴

又∵
 平分
平分
 平分
平分
∴

∴
 (2分)
(2分)在
 和
和 中,
中,
∴
 (4分)
(4分)(2)解:∵

∴

∵
 (7分)
(7分)∴

∴
 (8分)
(8分)(1)先利用角平分线性质、以及等量代换,可证出∠1=∠3,结合CD=CE,C是AB中点,即AC=BC,利用SAS可证全等;(2)利用角平分线性质,可知∠1=∠2,∠2=∠3,从而求出∠1=∠2=∠3,再利用全等三角形的性质可得出∠E=∠D,在△BCE中,利用三角形内角和是180°,可求出∠B

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
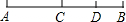 如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )
如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )| A、CD=AC-BD | ||
B、CD=
| ||
C、CD=
| ||
| D、CD=AD-BC |
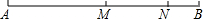

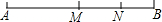 如图,M是线段AB的中点,N是线段MB的中点,且NB=6,求AB的长.
如图,M是线段AB的中点,N是线段MB的中点,且NB=6,求AB的长.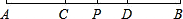 如图,P是线段AB的中点,点C、D把线段AB三等份.已知线段CP的长为2cm,求线段AB的长.
如图,P是线段AB的中点,点C、D把线段AB三等份.已知线段CP的长为2cm,求线段AB的长.