题目内容
【题目】在
中，
垂足为
.
(1)填空：
_________°；
(2)
是线段
上的动点，连结
，将线段绕点按顺时针方向旋转
，点
的对应点是点
，连接
，得到
.
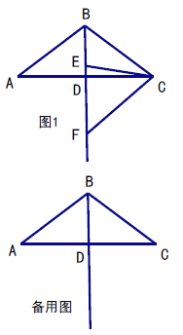
①如图1，若点在直线上，
，求
的值.
②连结
，直线A直线
是否平行，为什么？
【答案】(1)100；(2)①
；②
，见解析.
【解析】
（1）根据等腰三角形的性质和三角形内角和，计算解决即可；
（2）①根据等腰三角形三线合一的性质得出
，再结合旋转的性质得出
，根据线段间的数量关系求解即可；’
②根据题意，分类讨论进行证明，即分为：点F在BD上，点F在BD左侧，点F在BD右侧三种情况，根据平行线的判定定理进行证明即可.
解：(1)∵AB=BC
∴∠A=∠BCA
又∵∠A=40°，
∴∠ABC=18O°-40°-40°=100
(2)①在
中，
∴
∵
点F在BD上，∴
又
∴
∴
∴
.
②证明：连结
并延长交
于
若点
在直线
上，
是
的垂直平分线
∵
，又
∴
若点在直线的左侧，
，
∴
∴
∴.
若点在直线的右侧，
，
∴
∴
∴.
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
