题目内容
如图，点D在AC的垂直平分线上，AB∥CD，若∠D=130°，则∠BAC=
- A.15°
- B.20°
- C.25°
- D.30°
C
分析：根据线段垂直平分线的性质可得∠DAC=∠DCA，再利用三角形内角和定理求得∠DCA的度数，再利用两直线平行内错角相等即可求得∠BAC的度数．
解答：解；∵点D在AC的垂直平分线上，
∴AD=CD，
∴∠DAC=∠DCA，
∵∠D=130°，
∴∠DAC=∠DCA=
（180-130）=25°，
∵AB∥CD，
∴∠BAC=∠DCA=25°，
故选C．
点评：此题主要考查线段垂直平分线的性质，三角形内角和定理，平行线的性质等知识点，难度不大，都是些基础知识，要求学生应熟练掌握．
分析：根据线段垂直平分线的性质可得∠DAC=∠DCA，再利用三角形内角和定理求得∠DCA的度数，再利用两直线平行内错角相等即可求得∠BAC的度数．
解答：解；∵点D在AC的垂直平分线上，
∴AD=CD，
∴∠DAC=∠DCA，
∵∠D=130°，
∴∠DAC=∠DCA=
（180-130）=25°，∵AB∥CD，
∴∠BAC=∠DCA=25°，
故选C．
点评：此题主要考查线段垂直平分线的性质，三角形内角和定理，平行线的性质等知识点，难度不大，都是些基础知识，要求学生应熟练掌握．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
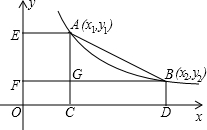积为14，那么双曲线的解析式为
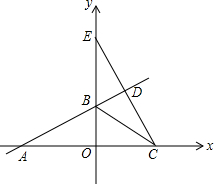B点C（4，O），过点C作AB的垂CD，点D为垂足，直线CD交y轴于点E，
如图，在同一平面内有A、B、C三个点，根据要求画图：
如图，点P在三角形ABC的边BC上．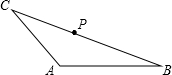
如图，点P在三角形ABC的边BC上．