Question

【题目】设、、为实数，且，抛物线与轴交于、两点，与轴交于点，且抛物线的顶点在直线上.若是直角三角形，则面积的最大值是（ ）.

A.1B.

C.2D.3

Answer 1

【答案】A

【解析】

先根据已知条件设出抛物线与x轴的交点，由射影定理的逆定理可求出c2＝（x1）x2＝x1x2，由根与系数的关系及抛物线的顶点坐标可求出4a＝4＋b2，且a≥1，再由三角形的面积公式及a的取值范围可求出其最大面积．

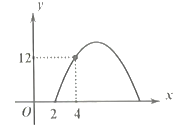
设y＝ax2＋bx＋c交y轴于点C（0，c），c≠0，交x轴于点A（x1，0）、B（x2，0），且x1＜0＜x2，

由△ABC是直角三角形知，点C必为直角顶点，且c2＝（x1）x2＝x1x2（射影定理的逆定理），

由根与系数的关系得，x1＋x2＝，x1x2＝，

所以c2＝，c＝，

又＝1，即4a＝4＋b2，且a≥1，

所以S△ABC＝|c||x1x2|＝ (x1＋x2)24x1x2，

＝，

＝≤1，

当且仅当a＝1，b＝0，c＝1时等号成立，因此，Rt△ABC的最大面积是1．

故选：A．