题目内容
已知cosα=
,则
的值等于( )
| 1 |
| 3 |
| 3sinα-tanα |
| 4sinα+2tanα |
A、
| ||
B、
| ||
C、
| ||
| D、0 |
分析:(1)画出直角三角形,根据cosα=
及三角函数的定义求出各三角函数的值再进行计算.
(2)分子分母都除以sinα,将原式转化为关于cosα的代数式,再将cosα=
代入求值即可.
| 1 |
| 3 |
(2)分子分母都除以sinα,将原式转化为关于cosα的代数式,再将cosα=
| 1 |
| 3 |
解答: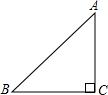 解:(1)如图:设∠B=α,根据cosα=
解:(1)如图:设∠B=α,根据cosα=
,设BC=x,AB=3x,则AC=
=2
x.
所以sinα=
=
,tanα=
=2
,
于是原式=
=
=0.
(2)分子分母都除以sinα,原式=
=
①,
∵cosα=
,
∴
=3,
∴原式=
=0.
 解:(1)如图:设∠B=α,根据cosα=
解:(1)如图:设∠B=α,根据cosα=| 1 |
| 3 |
| (3x)2-x2 |
| 2 |
所以sinα=
2
| ||
| 3x |
2
| ||
| 3 |
2
| ||
| x |
| 2 |
于是原式=
3×
| ||||||||
4×
|
| 0 | ||||||||
4×
|
(2)分子分母都除以sinα,原式=
3-
| ||
4+
|
3-
| ||
4+
|
∵cosα=
| 1 |
| 3 |
∴
| 1 |
| cosα |
∴原式=
| 3-3 |
| 4+2×3 |
点评:此题考查了同角三角函数的关系.
方法(1)画出图形,利用三角函数的定义求出各特殊角的三角函数值即可解答此题.
方法(2)需要将tanα转化为
,利用分式性质和cosα=
解答.
方法(1)画出图形,利用三角函数的定义求出各特殊角的三角函数值即可解答此题.
方法(2)需要将tanα转化为
| sinα |
| cosα |
| 1 |
| 3 |

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 已知AB是⊙O的直径,弦AC与BD交于点P,若CD=5,AB=13,则cos∠APD等于( )
已知AB是⊙O的直径,弦AC与BD交于点P,若CD=5,AB=13,则cos∠APD等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
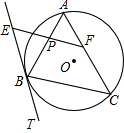
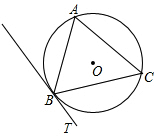
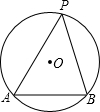 如图所示,已知AB是⊙O中一条长为4的弦,P是⊙O上一动点,且
如图所示,已知AB是⊙O中一条长为4的弦,P是⊙O上一动点,且