题目内容
6.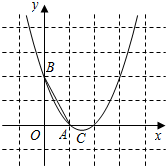 如图,已知抛物线y=x2+bx+c经过A(1,0),B(0,2)两点,顶点为C.
如图,已知抛物线y=x2+bx+c经过A(1,0),B(0,2)两点,顶点为C.(1)求抛物线的解析式;
(2)求△ABC的面积.
分析 (1)直接把A(1,0),B(0,2)代入y=x2+bx+c得到关于b、c的方程组,解方程组求出b、c,可确定抛物线的解析式;
(2)把(1)的解析式进行配方可得到顶点式,得到顶点坐标,然后根据△ABC的面积等于一个大的三角形的面积减去一个小的三角形的面积和一个梯形的面积求得即可.
解答 解:(1)把A(1,0),B(0,2)代入y=x2+bx+c
$\left\{\begin{array}{l}{1+b+c=0}\\{c=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-3}\\{c=2}\end{array}\right.$.
故抛物线的解析式为y=x2-3x+2;
(2)∵y=x2-3x+2=(x-$\frac{3}{2}$)2-$\frac{1}{4}$,
∴顶点C的坐标为($\frac{3}{2}$,-$\frac{1}{4}$),
S△ABC=$\frac{1}{2}$(2+$\frac{1}{4}$)×$\frac{3}{2}$-$\frac{1}{2}$×1×2-$\frac{1}{2}$(1+$\frac{3}{2}$)×$\frac{1}{4}$=$\frac{3}{8}$.
点评 本题考查了待定系数法求二次函数的解析式:先设抛物线的解析式(一般式、顶点式或交点式),再把抛物线上的点的坐标代入得到方程组,然后解方程可确定抛物线的解析式.也考查了二次函数的性质.

练习册系列答案
相关题目
10.“十•一”黄金周期间,九寨沟风景区在7天假期中每天旅游的人数变化如表:(正数表示比9月30日多的人数,负数表示比9月30日少的人数):
(1)若9月30日的游客人数记为a万人,请用含a的代数式表示10月2日的游客人数;
(2)请判断7天内游客人数最多和最少的各是哪一天,它们相差多少万人?
(2)若a=2,平均每人消费300元,请问风景区在这7天内总收入多少万元?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 (万人) | +1.7 | +0.9 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)请判断7天内游客人数最多和最少的各是哪一天,它们相差多少万人?
(2)若a=2,平均每人消费300元,请问风景区在这7天内总收入多少万元?
17. 如图,在平面直角坐标系中.矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.如果OA=3,OC=2,则经过点E的反比例函数解析式为( )
如图,在平面直角坐标系中.矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.如果OA=3,OC=2,则经过点E的反比例函数解析式为( )
 如图,在平面直角坐标系中.矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.如果OA=3,OC=2,则经过点E的反比例函数解析式为( )
如图,在平面直角坐标系中.矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.如果OA=3,OC=2,则经过点E的反比例函数解析式为( )| A. | $y=\frac{9}{2x}$ | B. | $y=\frac{2}{9x}$ | C. | $y=\frac{{\sqrt{13}}}{x}$ | D. | $y=\frac{{\sqrt{13}}}{2x}$ |
14.某校八年级(1)班50名学生参加2007年济宁市数学质量监测考试,全班学生的成绩统计如下表:
请根据表中提供的信息解答下列问题:
(1)该班学生考试成绩的众数和中位数分别是多少?
(2)该班张华同学在这次考试中的成绩是83分,能不能说张华同学的成绩处于全班中偏上水平?试说明理由.
| 成绩(分) | 71 | 74 | 78 | 80 | 82 | 83 | 85 | 86 | 88 | 90 | 91 | 92 | 94 |
| 人数 | 1 | 2 | 3 | 5 | 4 | 5 | 3 | 7 | 8 | 4 | 3 | 3 | 2 |
(1)该班学生考试成绩的众数和中位数分别是多少?
(2)该班张华同学在这次考试中的成绩是83分,能不能说张华同学的成绩处于全班中偏上水平?试说明理由.
1.随意掷两个均匀的骰子,朝上面的点数之和是10的概率是( )
| A. | $\frac{1}{12}$ | B. | 1 | C. | $\frac{1}{18}$ | D. | 0 |
15.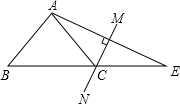 如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
 如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )| A. | 45° | B. | 60° | C. | 50° | D. | 55° |
 如图半径是13cm圆柱形油槽,装入油后,油深CD为5cm,求油面宽度AB.
如图半径是13cm圆柱形油槽,装入油后,油深CD为5cm,求油面宽度AB.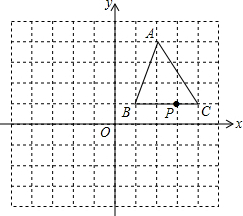 如图,三角形ABC的顶点坐标分别为A(2,4)、B(1,1)、C(4,1).BC上的一点P的坐标为P(3,1),将三角形ABC向左平移4个单位,再向上平移1个单位,得到三角形A1B1C1,其中点A、B、C、P分别对应点A1、B1、C1、P1.
如图,三角形ABC的顶点坐标分别为A(2,4)、B(1,1)、C(4,1).BC上的一点P的坐标为P(3,1),将三角形ABC向左平移4个单位,再向上平移1个单位,得到三角形A1B1C1,其中点A、B、C、P分别对应点A1、B1、C1、P1.