题目内容
 如图,直线y=kx+6与x、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0),P(x,y)是直线y=kx+6上的一个动点.
如图,直线y=kx+6与x、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0),P(x,y)是直线y=kx+6上的一个动点.(1)求k的值;
(2)若点P是第二象限内的直线上的一个动点,当点P运动过程中,试写出三角形OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,三角形OPA的面积为
| 27 | 8 |
分析:(1)将点E的坐标(-8,0)代入直线y=kx+6,得到关于k的方程,解方程即可求出k的值;
(2)由点A的坐标为(-6,0)得到OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式表示出△OPA的面积,从而求出其关系式;根据P点运动的范围可求出自变量x的取值范围;
(3)根据三角形的面积公式,由△OPA的面积为
,列出关于点P的纵坐标y的方程,解方程求出y的值,再代入直线的解析式求出x的值,即可得到P点的坐标.
(2)由点A的坐标为(-6,0)得到OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式表示出△OPA的面积,从而求出其关系式;根据P点运动的范围可求出自变量x的取值范围;
(3)根据三角形的面积公式,由△OPA的面积为
| 27 |
| 8 |
解答:解:(1)∵点E(-8,0)在直线y=kx+6上,
∴0=-8k+6,
∴k=
;
 (2)∵k=
(2)∵k=
,
∴直线的解析式为:y=
x+6,
∵点P(x,y)是第二象限内的直线y=
x+6上的一个动点,
∴y=
x+6>0,-8<x<0.
∵点A的坐标为(-6,0),
∴OA=6,
∴S=
OA•|yP|=
×6×(
x+6)=
x+18.
∴三角形OPA的面积S与x的函数关系式为:S=
x+18(-8<x<0);
(3)∵三角形OPA的面积=
OA•|yP|=
,P(x,y),
∴
×6×|y|=
,
解得|y|=
,
∴y=±
.
当y=
时,
=
x+6,
解得x=-
,故P(-
,
);
当y=-
时,-
=
x+6,
解得x=-
,故P(-
,-
);
综上可知,当点P的坐标为P(-
,
)或P(-
,-
)时,三角形OPA的面积为
.
∴0=-8k+6,
∴k=
| 3 |
| 4 |
 (2)∵k=
(2)∵k=| 3 |
| 4 |
∴直线的解析式为:y=
| 3 |
| 4 |
∵点P(x,y)是第二象限内的直线y=
| 3 |
| 4 |
∴y=
| 3 |
| 4 |
∵点A的坐标为(-6,0),
∴OA=6,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 9 |
| 4 |
∴三角形OPA的面积S与x的函数关系式为:S=
| 9 |
| 4 |
(3)∵三角形OPA的面积=
| 1 |
| 2 |
| 27 |
| 8 |
∴
| 1 |
| 2 |
| 27 |
| 8 |
解得|y|=
| 9 |
| 8 |
∴y=±
| 9 |
| 8 |
当y=
| 9 |
| 8 |
| 9 |
| 8 |
| 3 |
| 4 |
解得x=-
| 13 |
| 2 |
| 13 |
| 2 |
| 9 |
| 8 |
当y=-
| 9 |
| 8 |
| 9 |
| 8 |
| 3 |
| 4 |
解得x=-
| 19 |
| 2 |
| 19 |
| 2 |
| 9 |
| 8 |
综上可知,当点P的坐标为P(-
| 13 |
| 2 |
| 9 |
| 8 |
| 19 |
| 2 |
| 9 |
| 8 |
| 27 |
| 8 |
点评:本题是一次函数的综合题,考查了一次函数图象上点的坐标特征,三角形面积公式的运用,难度适中.注意第三问中的点P(x,y)是直线y=kx+6上的一个动点,不能直接代入第二问所求的函数解析式,否则漏解,这是本题容易弄错的地方.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
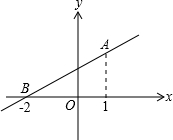 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为