题目内容
如图，在四边形ABCD中，∠A=∠C=90°，且BD平分∠ABC，BD=3，BC=2，AD的长度为（ ）| A、1 | ||
B、
| ||
C、
| ||
| D、5 |
考点：角平分线的性质,勾股定理
专题：
分析：利用勾股定理列式求出CD，再根据角平分线上的点到角的两边距离相等可得AD=CD．
解答：解：∵BD=3，BC=2，∠C=90°，
∴CD=
=
=
，
∵∠A=∠C=90°，且BD平分∠ABC，
∴AD=CD=
．
故选B．
∴CD=
| BD2-BC2 |
| 32-22 |
| 5 |
∵∠A=∠C=90°，且BD平分∠ABC，
∴AD=CD=
| 5 |
故选B．
点评：本题考查了角平分线上的点到角的两边距离相等的性质，勾股定理，熟记性质是解题的关键．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
已知，如图，直线AB、CD交于点O，OE⊥AB于O，∠COE=50°，则∠BOD=坐标平面上有一点A，且A点到x轴的距离为3，A点到y轴的距离为到x轴距离的2倍．若A点在第二象限，则A点坐标为（ ）
| A、（-3，6） |
| B、（-3，2） |
| C、（-6，3） |
| D、（-2，3） |
要了解全校2000名学生课外作业负担情况，你认为以下抽样方法中比较合理的是（ ）
| A、调查全体女生 |
| B、调查全体男生 |
| C、调查九年级全体学生 |
| D、调查各年级中的部分学生 |
如图，函数y=ax-1的图象过点（1，2），则不等式ax-1＞2的解集是（ ）| A、x＜1 | B、x＞1 |
| C、x＜2 | D、x＞2 |
某股民用30000元买进甲、乙两种股票，在甲股票下跌10%，乙股票升值8%时全部卖出，赚得1500元（含税），则该股民原来购买的甲、乙两种股票所用钱数的比例为（ ）
| A、2：3 | B、3：2 |
| C、1：5 | D、5：1 |
如果不等式组
有解，那么m的取值范围是（ ）
|
| A、m＞5 | B、m＜5 |
| C、m≥5 | D、m≤5 |
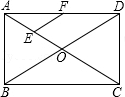如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6cm，BC=8cm，则△AEF的周长为（ ）| A、7cm | B、8cm |
| C、9cm | D、12cm |