题目内容
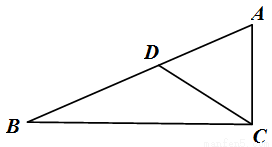
(10分)已知:如图,在 中,D是AC上一点,E是AB上一点,且∠AED=∠C.
中,D是AC上一点,E是AB上一点,且∠AED=∠C.

(1)求证:△AED∽△ACB;(4分)
(2)若AB=6,AD=4,AC=5,求AE的长。(6分)
(2)
【解析】
试题分析:(1)根据两角对应相等的两三角形相似的判定可直接证得结果△AED∽△ACB;
(2)根据相似三角形的性质可由△AED∽△ACB得 ,然后代入已知的值可求得AE的长.
,然后代入已知的值可求得AE的长.
试题解析:(1)证明:∵∠A=∠A,∠AED=∠C,
∴△AED∽△ACB。
(2)【解析】
∵△AED∽△ACB,
∴
∴
∴
考点:相似三角形的性质与判定
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边.
相邻两边的公共端点叫做三角形的顶点.
相邻两边组成的角叫做三角形的内角,简称三角形的角.
(2)按边的相等关系分类:不等边三角形和等腰三角形(底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形).
(3)三角形的主要线段:角平分线、中线、高.
(4)三角形具有稳定性. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 , 求
, 求 的值.
的值. ,则该扇形的半径是 。
,则该扇形的半径是 。 与二次函数
与二次函数 在同一平面直角坐标系中的图象可能是( )
在同一平面直角坐标系中的图象可能是( )