Question

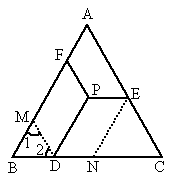
在一块等边三角形的草坪上，修建了一座凉亭，地点设为P，并从P点出发，分别修出一条通往等边三角形边缘的小路，为了美观，修小路要求PE∥BC、PD∥AB、PF∥AC，如图所示，若已知等边三角形的周长为1800m．

求：(1)三条小路PE、PD、PF的和；

(2)如果小路宽均为1m，每块砖的正面面积为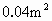，求需要多少块砖？

Answer 1

答案：600m:15000块
解析：

解：(1)方法一：分别过点D、E作DM∥PF，EN∥PD，分别交AB于点M，BC于点N 因为PD∥MF，PE∥DN， 所以四边形FMDP与四边形PDNE是平行四边形， 所以PF=MD，PE=DN，PD=NE． 因为△ABC是等边三角形， 所以∠B=∠C=∠A=60°． 因为MD∥FP，FP∥AC， 所以MD∥AC， 所以∠1=∠A=60°，∠2=∠C=60°， 所以△MBD是等边三角形， 所以MD=DB，同理EN=NC． 所以PF＋PE＋PD=MD＋DN＋NE=BD＋DN＋NC=BC， 因为△ABC的周长为1800m， 所以BC=600m， 所以PF＋PE＋PD=600m， 方法二：如图所示， 延长FP交BC于点M，延长EP交AB于点N． 因为FM∥AC，NE∥BC，PD∥AB， 所以四边形NBDP，PMCE是平行四边形， 所以PN=BD，PE=MC． 因为△ABC是等边三角形， 所以∠A=∠B=∠C=60°， 所以∠1=∠2=∠3=∠4=60°， 所以△FNP，△PDM是等边三角形， 所以PF=PN，PD=DM， 所以PF＋PD＋PE=PN＋DM＋MC=BD＋DM＋MC=BC． 因为△ABC周长为1800m， 所以BC=600m， 所以PF＋PD＋PE=600m (2)小路面积=(PE＋PF＋PD)×路宽=600×1=600()． 所以砖数为600÷0.04=15000(块)．